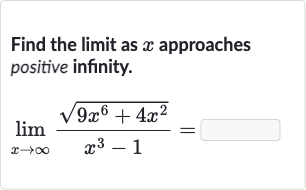Find the limit as x approaches positive infinity. lim_(x rarr oo)(sqrt(9x^(6)+4x^(2)))/(x^(3)-1)=

Question

Find the limit as  x approaches positive infinity.  lim_(x rarr oo)(sqrt(9x^(6)+4x^(2)))/(x^(3)-1)=

Bytelearn · Accepted Answer

Identify highest power of x: Identify the highest power of x in the numerator and denominator. In the expression (sqrt(9x^(6)+4x^(2)))/(x^(3)-1), the highest power of x in the numerator inside the square root is x^6, which is equivalent to x^3 when taken out of the square root. In the denominator, the highest power of x is x^3.Divide numerator and denominator: Divide the numerator and the denominator by the highest power of x in the denominator. To simplify the limit, we divide every term by x^3, which is the highest power of x in the denominator. lim_(x rarr oo)(sqrt(9x^(6)+4x^(2)))/(x^(3)-1) = lim_(x rarr oo)(sqrt((9x^(6)/x^(6))+(4x^(2)/x^(6))))/((x^(3)/x^(3))-(1/x^(3)))Simplify expression inside the limit: Simplify the expression inside the limit. After dividing by x^3, we get: lim_(x rarr oo)(sqrt(9+(4/x^(4))))/(1-(1/x^(3))) Now, as x approaches infinity, (4/x^(4)) and (1/x^(3)) approach 0.Evaluate the limit: Evaluate the limit as x approaches infinity. lim_(x rarr oo)(sqrt(9+(4/x^(4))))/(1-(1/x^(3))) = sqrt(9+0)/(1-0) = sqrt(9)/1 = 3

Find the limit as $x$ approaches positive infinity. $\newline$ $\lim _{x \rightarrow \infty} \frac{\sqrt{9 x^{6}+4 x^{2}}}{x^{3}-1}=$

Full solution

More problems from Powers with decimal and fractional bases

Related topics

Find the limit as x x x approaches positive infinity.\newlinelim⁡x→∞9x6+4x2x3−1= \lim _{x \rightarrow \infty} \frac{\sqrt{9 x^{6}+4 x^{2}}}{x^{3}-1}= x→∞lim​x3−19x6+4x2​​=

Find the limit as $x$ approaches positive infinity. $\newline$ $\lim _{x \rightarrow \infty} \frac{\sqrt{9 x^{6}+4 x^{2}}}{x^{3}-1}=$