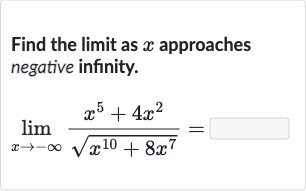Find the limit as x approaches negative infinity. lim_(x rarr-oo)(x^(5)+4x^(2))/(sqrt(x^(10)+8x^(7)))=

Question

Find the limit as  x approaches negative infinity.  lim_(x rarr-oo)(x^(5)+4x^(2))/(sqrt(x^(10)+8x^(7)))=

Bytelearn · Accepted Answer

Analyze Function and Limit: Analyze the given function and the limit to be found. We need to find the limit of the function (x^5 + 4x^2) / (sqrt(x^10 + 8x^7)) as x approaches negative infinity. To do this, we will look for the dominant terms in the numerator and the denominator.Identify Dominant Terms: Identify the dominant terms in the numerator and the denominator. In the numerator, the dominant term is x^5 because it has the highest power of x. In the denominator, the dominant term inside the square root is x^10, which is the highest power of x there.Simplify by Dividing: Simplify the function by dividing the numerator and the denominator by x^5. We divide each term in the numerator and the square root of each term in the denominator by x^5 to simplify the expression. This gives us:  lim_(x rarr-oo) (x^5/x^5 + 4x^2/x^5) / (sqrt(x^10/x^5 + 8x^7/x^5))  Simplifying further, we get:  lim_(x rarr-oo) (1 + 4/x^3) / (sqrt(x^5 + 8x^2))Evaluate Limit: Evaluate the limit of the simplified function as x approaches negative infinity. As x approaches negative infinity, the terms 4/x^3 and 8x^2/x^5 in the simplified function will approach 0 because they have x in the denominator with a positive power. This leaves us with:  lim_(x rarr-oo) 1 / sqrt(x^5)  Since x is approaching negative infinity, we need to consider the behavior of sqrt(x^5). The square root function is not defined for negative numbers, but since we are dealing with x^5, which is an odd power, the result will be negative and the square root of a negative number is not a real number. This indicates that we have made a mistake in our simplification process because we cannot take the square root of a negative number.

Find the limit as $x$ approaches negative infinity. $\newline$ $\lim _{x \rightarrow-\infty} \frac{x^{5}+4 x^{2}}{\sqrt{x^{10}+8 x^{7}}}=$

Full solution

More problems from Powers with decimal and fractional bases

Related topics

Find the limit as x x x approaches negative infinity.\newlinelim⁡x→−∞x5+4x2x10+8x7= \lim _{x \rightarrow-\infty} \frac{x^{5}+4 x^{2}}{\sqrt{x^{10}+8 x^{7}}}= x→−∞lim​x10+8x7​x5+4x2​=

Find the limit as $x$ approaches negative infinity. $\newline$ $\lim _{x \rightarrow-\infty} \frac{x^{5}+4 x^{2}}{\sqrt{x^{10}+8 x^{7}}}=$