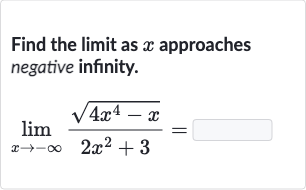Find the limit as x approaches negative infinity. lim_(x rarr-oo)(sqrt(4x^(4)-x))/(2x^(2)+3)=

Question

Find the limit as  x approaches negative infinity.  lim_(x rarr-oo)(sqrt(4x^(4)-x))/(2x^(2)+3)=

Bytelearn · Accepted Answer

Identify highest power of x: Identify the highest power of x in the numerator and denominator. In the expression (sqrt(4x^(4)-x))/(2x^(2)+3), the highest power of x in the numerator inside the square root is x^4, and the highest power of x in the denominator is x^2.Divide numerator and denominator: Divide the numerator and the denominator by the highest power of x in the denominator. To simplify the limit, we divide every term by x^2, which is the highest power of x in the denominator. lim_(x rarr-oo)(sqrt(4x^(4)/x^2 - x/x^2))/(2x^(2)/x^2 + 3/x^2)Simplify expression inside the limit: Simplify the expression inside the limit. After dividing by x^2, the expression becomes: lim_(x rarr-oo)(sqrt(4x^2 - 1/x^2))/(2 + 3/x^2)Evaluate limit as x approaches negative infinity: Evaluate the limit as x approaches negative infinity. As x approaches negative infinity, the terms -1/x^2 and 3/x^2 approach 0. Therefore, the expression simplifies to: lim_(x rarr-oo)(sqrt(4x^2))/(2)Simplify square root and expression: Simplify the square root and the expression. Since sqrt(4x^2) = 2|x| and we are considering x approaching negative infinity, |x| = -x. Therefore, the expression becomes: lim_(x rarr-oo)(2(-x))/(2)Simplify expression further: Simplify the expression further. The 2's cancel out, and we are left with: lim_(x rarr-oo)(-x)Evaluate final limit: Evaluate the final limit. As x approaches negative infinity, -x approaches positive infinity. Therefore, the limit is: lim_(x rarr-oo)(-x) = +oo

Find the limit as $x$ approaches negative infinity. $\newline$ $\lim _{x \rightarrow-\infty} \frac{\sqrt{4 x^{4}-x}}{2 x^{2}+3}=$

Full solution

More problems from Powers with decimal and fractional bases

Related topics

Find the limit as x x x approaches negative infinity.\newlinelim⁡x→−∞4x4−x2x2+3= \lim _{x \rightarrow-\infty} \frac{\sqrt{4 x^{4}-x}}{2 x^{2}+3}= x→−∞lim​2x2+34x4−x​​=

Find the limit as $x$ approaches negative infinity. $\newline$ $\lim _{x \rightarrow-\infty} \frac{\sqrt{4 x^{4}-x}}{2 x^{2}+3}=$