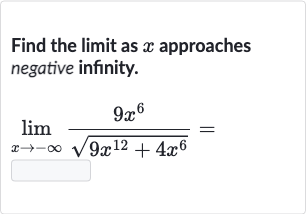Find the limit as x approaches negative infinity. lim_(x rarr-oo)(9x^(6))/(sqrt(9x^(12)+4x^(6)))=

Question

Find the limit as  x approaches negative infinity.  lim_(x rarr-oo)(9x^(6))/(sqrt(9x^(12)+4x^(6)))=

Bytelearn · Accepted Answer

Identify highest power of x: Identify the highest power of x in the numerator and denominator. In the expression (9x^(6))/(sqrt(9x^(12)+4x^(6))), the highest power of x in the numerator is x^6. In the denominator, after simplifying the square root, the highest power of x will also be x^6.Factor out highest power of x: Factor out the highest power of x from the square root in the denominator. To simplify the expression, we can factor x^6 out of the square root in the denominator, which gives us x^6 * sqrt(9 + 4/x^(6)).Simplify expression by canceling factors: Simplify the expression by canceling out common factors. The x^6 in the numerator and the x^6 that was factored out of the square root in the denominator will cancel each other out. This leaves us with (9)/(sqrt(9 + 4/x^(6))).Evaluate limit as x approaches negative infinity: Evaluate the limit as x approaches negative infinity. As x approaches negative infinity, the term 4/x^(6) approaches 0 because any finite number divided by an infinitely large number tends to 0. Therefore, the expression inside the square root becomes sqrt(9 + 0), which simplifies to sqrt(9).Calculate final value of the limit: Calculate the final value of the limit. The final value of the limit is (9)/(sqrt(9)), which simplifies to (9)/(3) because sqrt(9) is 3. Therefore, the limit is 3.

Find the limit as $x$ approaches negative infinity. $\newline$ $\lim _{x \rightarrow-\infty} \frac{9 x^{6}}{\sqrt{9 x^{12}+4 x^{6}}}=$

Full solution

More problems from Powers with decimal and fractional bases

Related topics

Find the limit as x x x approaches negative infinity.\newlinelim⁡x→−∞9x69x12+4x6= \lim _{x \rightarrow-\infty} \frac{9 x^{6}}{\sqrt{9 x^{12}+4 x^{6}}}= x→−∞lim​9x12+4x6​9x6​=

Find the limit as $x$ approaches negative infinity. $\newline$ $\lim _{x \rightarrow-\infty} \frac{9 x^{6}}{\sqrt{9 x^{12}+4 x^{6}}}=$