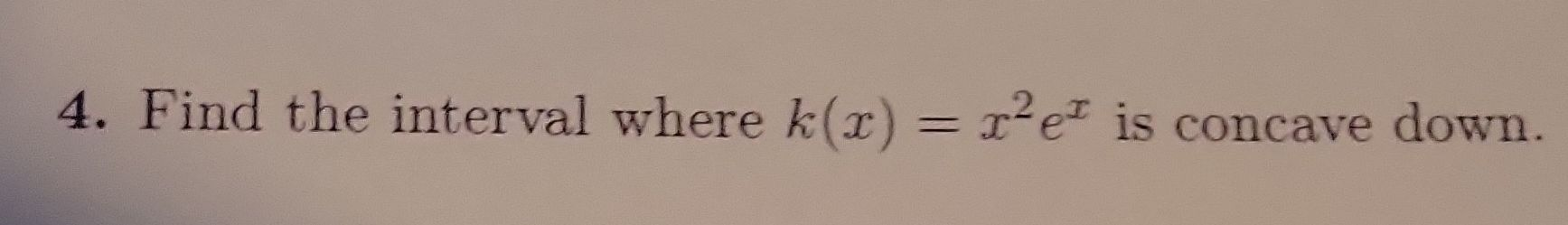Find the interval where $k(x)=x^{2} e^{x}$ is concave down.

View step-by-step help

Home

Math Problems

Calculus

Find derivatives of logarithmic functions

Full solution

Q. Find the interval where

k(x)=x^{2} e^{x}

is concave down.

Find First Derivative: To determine where the function $k(x) = x^{2}e^{x}$ is concave down, we need to find the second derivative of $k(x)$ and then find the interval where this second derivative is negative.
Find Second Derivative: First, let's find the first derivative $k'(x)$ using the product rule, which states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.
Analyze Sign of Expression: Applying the product rule to $k(x) = x^{2}e^{x}$ , we get: $\newline$ $k'(x) = \frac{d}{dx}(x^{2}) \cdot e^{x} + x^{2} \cdot \frac{d}{dx}(e^{x})$ $\newline$ $k'(x) = 2x \cdot e^{x} + x^{2} \cdot e^{x}$ $\newline$ $k'(x) = e^{x}(2x + x^{2})$
Find Roots of Quadratic: Now, let's find the second derivative $k''(x)$ by differentiating $k'(x)$ . We will again use the product rule.
Apply Quadratic Formula: Differentiating $k'(x) = e^{x}(2x + x^{2})$ , we get: $\newline$ $k''(x) = \frac{d}{dx}(e^{x}) \cdot (2x + x^{2}) + e^{x} \cdot \frac{d}{dx}(2x + x^{2})$ $\newline$ $k''(x) = e^{x}(2x + x^{2}) + e^{x}(2 + 2x)$ $\newline$ $k''(x) = e^{x}(2 + 4x + x^{2})$
Determine Concave Down Interval: To find where $k''(x)$ is negative, we need to analyze the sign of the expression inside the parentheses, since $e^{x}$ is always positive for all $x$ .
Determine Concave Down Interval: To find where $k''(x)$ is negative, we need to analyze the sign of the expression inside the parentheses, since $e^{x}$ is always positive for all $x$ .We need to find the roots of the quadratic equation $2 + 4x + x^{2} = 0$ to determine the intervals where the expression is negative.
Determine Concave Down Interval: To find where $k''(x)$ is negative, we need to analyze the sign of the expression inside the parentheses, since $e^{x}$ is always positive for all $x$ .We need to find the roots of the quadratic equation $2 + 4x + x^{2} = 0$ to determine the intervals where the expression is negative.The quadratic equation can be rewritten as $x^{2} + 4x + 2 = 0$ . To solve for $x$ , we can use the quadratic formula $x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}$ , where $a = 1$ , $b = 4$ , and $c = 2$ .
Determine Concave Down Interval: To find where $k''(x)$ is negative, we need to analyze the sign of the expression inside the parentheses, since $e^{x}$ is always positive for all $x$ .We need to find the roots of the quadratic equation $2 + 4x + x^{2} = 0$ to determine the intervals where the expression is negative.The quadratic equation can be rewritten as $x^{2} + 4x + 2 = 0$ . To solve for $x$ , we can use the quadratic formula $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$ , where $a = 1$ , $b = 4$ , and $c = 2$ .Plugging the values into the quadratic formula, we get: $\newline$ $e^{x}$ $0$ $\newline$ $e^{x}$ $1$ $\newline$ $e^{x}$ $2$ $\newline$ $e^{x}$ $3$ $\newline$ $e^{x}$ $4$
Determine Concave Down Interval: To find where $k''(x)$ is negative, we need to analyze the sign of the expression inside the parentheses, since $e^{x}$ is always positive for all $x$ .We need to find the roots of the quadratic equation $2 + 4x + x^{2} = 0$ to determine the intervals where the expression is negative.The quadratic equation can be rewritten as $x^{2} + 4x + 2 = 0$ . To solve for $x$ , we can use the quadratic formula $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$ , where $a = 1$ , $b = 4$ , and $c = 2$ .Plugging the values into the quadratic formula, we get: $\newline$ $e^{x}$ $0$ $\newline$ $e^{x}$ $1$ $\newline$ $e^{x}$ $2$ $\newline$ $e^{x}$ $3$ $\newline$ $e^{x}$ $4$ The roots of the quadratic equation are $e^{x}$ $5$ and $e^{x}$ $6$ . The quadratic function is concave up, which means it is negative between its roots.
Determine Concave Down Interval: To find where $k''(x)$ is negative, we need to analyze the sign of the expression inside the parentheses, since $e^{x}$ is always positive for all $x$ .We need to find the roots of the quadratic equation $2 + 4x + x^{2} = 0$ to determine the intervals where the expression is negative.The quadratic equation can be rewritten as $x^{2} + 4x + 2 = 0$ . To solve for $x$ , we can use the quadratic formula $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$ , where $a = 1$ , $b = 4$ , and $c = 2$ .Plugging the values into the quadratic formula, we get: $\newline$ $e^{x}$ $0$ $\newline$ $e^{x}$ $1$ $\newline$ $e^{x}$ $2$ $\newline$ $e^{x}$ $3$ $\newline$ $e^{x}$ $4$ The roots of the quadratic equation are $e^{x}$ $5$ and $e^{x}$ $6$ . The quadratic function is concave up, which means it is negative between its roots.Therefore, the function $e^{x}$ $7$ is concave down on the interval $e^{x}$ $8$ .

Find the interval where k(x)=x2ex k(x)=x^{2} e^{x} k(x)=x2ex is concave down.

Find the interval where $k(x)=x^{2} e^{x}$ is concave down.