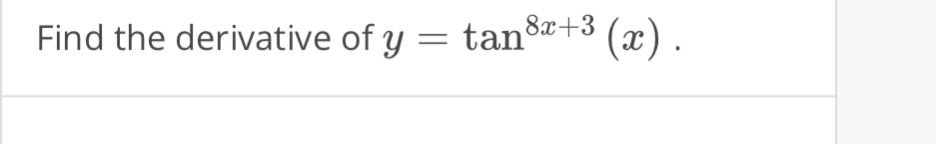Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the derivative of y=tan^(8x+3)(x).

Find the derivative of y=tan⁡8x+3(x) y=\tan ^{8 x+3}(x) .

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find derivatives using the chain rule Iright chevron icon

Full solution

Q. Find the derivative of y=tan⁡8x+3(x) y=\tan ^{8 x+3}(x) .
  1. Identify Function Components: Identify the function and its components.\newlineFunction y=tan⁡(8x+3)(x)y = \tan^{(8x+3)}(x) means y=(tan⁡(x))(8x+3)y = (\tan(x))^{(8x+3)}.
  2. Apply Chain Rule: Differentiate using the chain rule.\newlineLet u=tan⁡(x)u = \tan(x) and v=8x+3v = 8x+3. Then y=uvy = u^v.\newlinedydx=v⋅uv−1⋅dudx+uv⋅log⁡(u)⋅dvdx.\frac{dy}{dx} = v\cdot u^{v-1} \cdot \frac{du}{dx} + u^v \cdot \log(u) \cdot \frac{dv}{dx}.
  3. Calculate Derivatives: Calculate derivatives of uu and vv.dudx=sec⁡2(x)\frac{du}{dx} = \sec^2(x) (derivative of tan⁡(x)\tan(x)),dvdx=8\frac{dv}{dx} = 8 (derivative of 8x+38x+3).
  4. Substitute into Formula: Substitute back into the formula.\newlinedydx=(8x+3)⋅(tan⁡(x))8x+3−1⋅sec⁡2(x)+(tan⁡(x))8x+3⋅log⁡(tan⁡(x))⋅8.\frac{dy}{dx} = (8x+3) \cdot (\tan(x))^{8x+3-1} \cdot \sec^2(x) + (\tan(x))^{8x+3} \cdot \log(\tan(x)) \cdot 8.

More problems from Find derivatives using the chain rule I

Question
Find the derivative of f(x) f(x) .\newlinef(x)=cos⁡(x) f(x) = \cos(x) \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=tan⁡(x) f(x) = \tan(x) \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=ex f(x) = e^x \newlinef′(x)= f'\left(x\right) = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=ln⁡(x) f(x) = \ln(x) \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=tan⁡−1x f(x) = \tan^{-1}{x} \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=xex f(x) = x e^x \newlinef′(x)= f'\left(x\right) = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the derivative of f(x) f(x) . \newlinef(x)=exx f(x) = \frac{e^x}{x} \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the derivative of f(x) f(x) . \newline f(x)=e(x+1) f(x) = e^{(x + 1)} \newline f′(x)= f'\left(x\right) = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
Find the derivative of f(x) f(x) . \newlinef(x)=x+3 f(x) = \sqrt{x+3} \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the derivative of g(x) g(x). \newline g(x)=ln⁡(2x) g(x) = \ln(2x) \newline g′(x)= g^{\prime}(x) = ______
Get tutor helpright-arrow

Posted 3 months ago

View all (70)