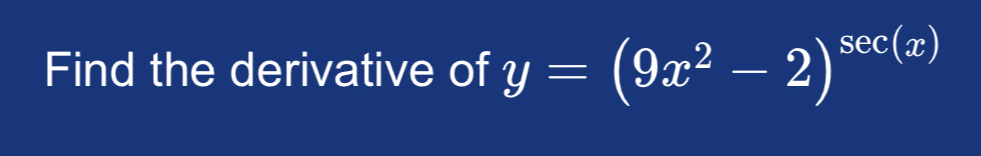Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the derivative of
y=(9x^(2)-2)^(sec(x))

Find the derivative of $y=\left(9 x^{2}-2\right)^{\sec (x)}$

View step-by-step help

View step-by-step help

Find derivatives of logarithmic functions

Full solution

Q. Find the derivative of

y=\left(9 x^{2}-2\right)^{\sec (x)}

Identify Function Type: Identify the type of function and the rule needed to differentiate it. $\newline$ We have a composite function where an inner function $9x^2 - 2$ is raised to the power of another function $\sec(x)$ . To differentiate this, we will need to use the chain rule and the product rule, as the exponent itself is a function of $x$ .
Apply Chain Rule: Apply the chain rule to differentiate the outer function with respect to the inner function. $\newline$ Let $u = 9x^2 - 2$ and $v = \sec(x)$ . Then $y = u^v$ . The derivative of $y$ with respect to $u$ is $v\cdot u^{(v-1)}$ by the power rule. We will later multiply this by the derivative of $u$ with respect to $x$ .
Differentiate Inner Function: Differentiate the inner function $u = 9x^2 - 2$ with respect to $x$ . The derivative of $u$ with respect to $x$ is $\frac{du}{dx} = 18x$ .
Apply Product Rule: Apply the product rule to differentiate the outer function with respect to $x$ . Since $y = u^v$ , we need to differentiate $v\cdot u^{(v-1)}$ with respect to $x$ . This requires the product rule because $v$ is a function of $x$ . The product rule states that $\frac{d(uv)}{dx} = u\frac{dv}{dx} + v\frac{du}{dx}$ .
Differentiate $\sec(x)$ : Differentiate $v = \sec(x)$ with respect to $x$ . The derivative of $\sec(x)$ with respect to $x$ is $\sec(x)\tan(x)$ . So $\frac{dv}{dx} = \sec(x)\tan(x)$ .
Apply Product Rule with Derivatives: Apply the product rule using the derivatives from steps $3$ and $5$ . $\newline$ We have $u = 9x^2 - 2$ , $\frac{du}{dx} = 18x$ , $v = \sec(x)$ , and $\frac{dv}{dx} = \sec(x)\tan(x)$ . Plugging these into the product rule, we get: $\newline$ $\frac{dy}{dx} = u^{(v-1)} * (v * \frac{du}{dx} + u * \frac{dv}{dx})$ $\newline$ $= (9x^2 - 2)^{(\sec(x)-1)} * (\sec(x) * 18x + (9x^2 - 2) * \sec(x)\tan(x))$
Simplify Expression: Simplify the expression for $\frac{dy}{dx}$ . $\frac{dy}{dx} = (9x^2 - 2)^{(\sec(x)-1)} \cdot (18x \cdot \sec(x) + (9x^2 - 2) \cdot \sec(x)\tan(x))$ This is the simplified form of the derivative.

More problems from Find derivatives of logarithmic functions

Question

Find the derivative of

f(x)

\newline

f(x) = \cos(x)

\newline

f'(x) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \ln(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan^{-1}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = x e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \frac{e^x}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^{(x + 1)}

\newline

f'\left(x\right) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \sqrt{x+3}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

g(x)

\newline

g(x) = \ln(2x)

\newline

g^{\prime}(x) =

Posted 3 months ago