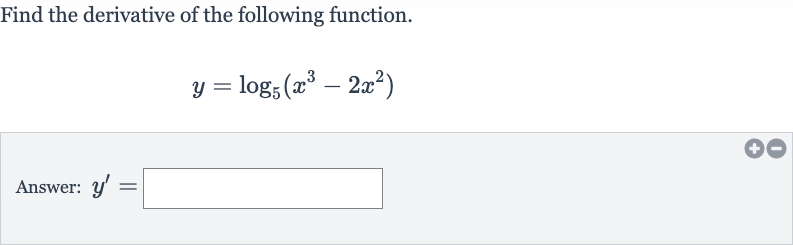
Find the derivative of the following function. y=log_(5)(x^(3)-2x^(2)) Answer: y^(')=

Question

Find the derivative of the following function.  y=log_(5)(x^(3)-2x^(2)) Answer:  y^(')=

Bytelearn · Accepted Answer

Understand function and base: Understand the function and the base of the logarithm. We are given the function y = log_5(x^3 - 2x^2), which is a logarithm with base 5. To find the derivative, we will need to use the change of base formula and the chain rule.Apply change of base: Apply the change of base formula to the logarithmic function. The change of base formula allows us to write the logarithm with base 5 in terms of the natural logarithm (ln): y = log_5(x^3 - 2x^2) = ln(x^3 - 2x^2) / ln(5)Differentiate using chain rule: Differentiate the function using the chain rule. To find y', we need to differentiate ln(x^3 - 2x^2) with respect to x and then divide by ln(5), which is a constant. Using the chain rule, the derivative of ln(u) with respect to x is (1/u) * du/dx, where u = x^3 - 2x^2.Calculate inner function derivative: Calculate the derivative of the inner function u = x^3 - 2x^2. The derivative of u with respect to x is du/dx = 3x^2 - 4x.Combine to find derivative: Combine the results to find the derivative of y. Now we can write the derivative of y as: y' = (1/(x^3 - 2x^2)) * (3x^2 - 4x) / ln(5)Simplify derivative expression: Simplify the derivative expression. We can leave the derivative in its current form, or we can simplify it further by distributing the numerator: y' = (3x^2 - 4x) / ((x^3 - 2x^2) * ln(5))

Find the derivative of the following function. $\newline$ $y=\log _{5}\left(x^{3}-2 x^{2}\right)$ $\newline$ Answer: $y^{\prime}=$

Full solution

More problems from Find derivatives of logarithmic functions

Related topics

Find the derivative of the following function.\newliney=log⁡5(x3−2x2) y=\log _{5}\left(x^{3}-2 x^{2}\right) y=log5​(x3−2x2)\newlineAnswer: y′= y^{\prime}= y′=

Find the derivative of the following function. $\newline$ $y=\log _{5}\left(x^{3}-2 x^{2}\right)$ $\newline$ Answer: $y^{\prime}=$