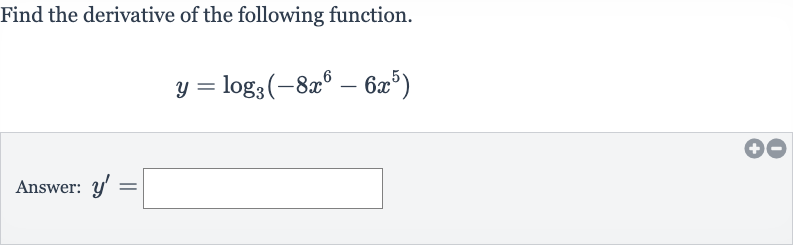
Find the derivative of the following function. y=log_(3)(-8x^(6)-6x^(5)) Answer: y^(')=

Question

Find the derivative of the following function.  y=log_(3)(-8x^(6)-6x^(5)) Answer:  y^(')=

Bytelearn · Accepted Answer

Identify Function & Derivative Type: Identify the function and the type of derivative to be found. We need to find the derivative of the function y = log_3(-8x^6 - 6x^5) with respect to x. This is a logarithmic differentiation problem where the base of the logarithm is 3.Apply Logarithmic Differentiation Rule: Apply the logarithmic differentiation rule. The derivative of log_b(u) with respect to x is (1/u) * (du/dx) * (1/log(b)), where u is a function of x and b is the base of the logarithm. In our case, u = -8x^6 - 6x^5 and b = 3.Differentiate Inside Function: Differentiate the inside function u = -8x^6 - 6x^5 with respect to x. Using the power rule, the derivative of u with respect to x is du/dx = -8 * 6x^(6-1) - 6 * 5x^(5-1) = -48x^5 - 30x^4.Substitute Derivative into Formula: Substitute the derivative of u into the differentiation formula. Now we have du/dx = -48x^5 - 30x^4, and we can substitute this into the formula from Step 2 to get the derivative of y with respect to x. y' = (1/(-8x^6 - 6x^5)) * (-48x^5 - 30x^4) * (1/log(3))Simplify Expression: Simplify the expression. We can simplify the expression by multiplying the terms together. However, we must be careful with the negative sign in the denominator. y' = (-48x^5 - 30x^4) / ((-8x^6 - 6x^5) * log(3))Factor Out Common Terms: Factor out common terms if possible. In this case, we can factor out an x^4 from the numerator and denominator to simplify the expression further. y' = (x^4(-48x - 30)) / (x^4(-8x^2 - 6x) * log(3)) y' = (-48x - 30) / ((-8x^2 - 6x) * log(3))Check for Simplifications: Check for any possible simplifications or cancellations. There are no further simplifications or cancellations that can be made in this expression. Therefore, the final derivative is: y' = (-48x - 30) / ((-8x^2 - 6x) * log(3))

Find the derivative of the following function. $\newline$ $y=\log _{3}\left(-8 x^{6}-6 x^{5}\right)$ $\newline$ Answer: $y^{\prime}=$

Full solution

More problems from Find derivatives of logarithmic functions

Related topics

Find the derivative of the following function.\newliney=log⁡3(−8x6−6x5) y=\log _{3}\left(-8 x^{6}-6 x^{5}\right) y=log3​(−8x6−6x5)\newlineAnswer: y′= y^{\prime}= y′=

Find the derivative of the following function. $\newline$ $y=\log _{3}\left(-8 x^{6}-6 x^{5}\right)$ $\newline$ Answer: $y^{\prime}=$