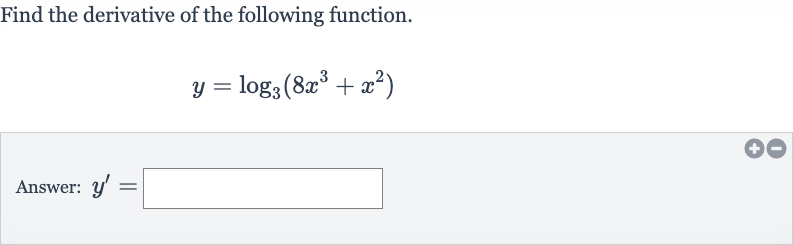
Find the derivative of the following function. y=log_(3)(8x^(3)+x^(2)) Answer: y^(')=

Question

Find the derivative of the following function.  y=log_(3)(8x^(3)+x^(2)) Answer:  y^(')=

Bytelearn · Accepted Answer

Identify Function & Derivative: Identify the function and the type of derivative needed. We need to find the derivative of the function y with respect to x, where y = log_3(8x^3 + x^2). This is a logarithmic differentiation problem with a base other than e.Apply Logarithmic Differentiation Rule: Apply the logarithmic differentiation rule. The derivative of log_b(u) with respect to x is (1/u) * (du/dx) * (1/log(b)), where u is a function of x and b is the base of the logarithm. In our case, u = 8x^3 + x^2 and b = 3.Differentiate Inside Function: Differentiate the inside function u = 8x^3 + x^2 with respect to x. Using the power rule, the derivative of u with respect to x is du/dx = 24x^2 + 2x.Substitute Derivative into Formula: Substitute the derivative of u into the formula from Step 2. We have du/dx = 24x^2 + 2x and u = 8x^3 + x^2. Substituting these into the formula gives us y' = (1/(8x^3 + x^2)) * (24x^2 + 2x) * (1/log(3)).Simplify Expression: Simplify the expression. We can simplify the expression by multiplying the terms together. This gives us y' = (24x^2 + 2x) / ((8x^3 + x^2) * log(3)).Check for Simplifications: Check for any possible simplifications. In this case, there is no further simplification that can be done without changing the expression significantly. So, we leave the derivative in its current form.

Find the derivative of the following function. $\newline$ $y=\log _{3}\left(8 x^{3}+x^{2}\right)$ $\newline$ Answer: $y^{\prime}=$

Full solution

More problems from Find derivatives of logarithmic functions

Related topics

Find the derivative of the following function.\newliney=log⁡3(8x3+x2) y=\log _{3}\left(8 x^{3}+x^{2}\right) y=log3​(8x3+x2)\newlineAnswer: y′= y^{\prime}= y′=

Find the derivative of the following function. $\newline$ $y=\log _{3}\left(8 x^{3}+x^{2}\right)$ $\newline$ Answer: $y^{\prime}=$