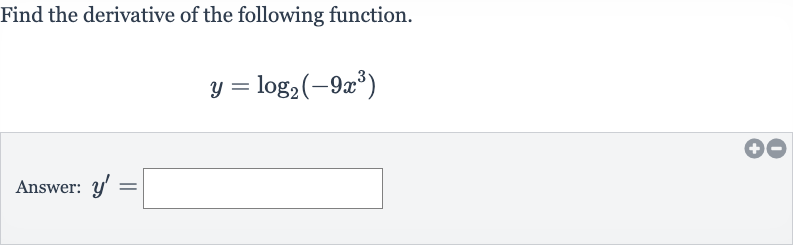
Find the derivative of the following function. y=log_(2)(-9x^(3)) Answer: y^(')=

Question

Find the derivative of the following function.  y=log_(2)(-9x^(3)) Answer:  y^(')=

Bytelearn · Accepted Answer

Identify Function: Identify the function and its components. We are given y = log_2(-9x^3), which is a logarithmic function with base 2. We need to find the derivative of this function with respect to x.Apply Rule: Apply the logarithmic differentiation rule. The derivative of log_b(u) with respect to x is (1/u) * (du/dx) * (1/log(b)), where u is a function of x and b is the base of the logarithm. In our case, u = -9x^3 and b = 2.Differentiate Inner Function: Differentiate the inner function u = -9x^3 with respect to x. The derivative of u with respect to x is du/dx = d/dx(-9x^3) = -27x^2.Substitute Derivative: Substitute the derivative of u into the differentiation formula. Using the result from Step 3, we substitute du/dx into the formula from Step 2 to get y' = (1/(-9x^3)) * (-27x^2) * (1/log(2)).Simplify Expression: Simplify the expression. We can simplify the expression by multiplying the terms together. This gives us y' = (-27x^2 / (-9x^3)) * (1/log(2)) = 3/x * (1/log(2)).Check for Errors: Check for any mathematical errors. There are no mathematical errors in the previous steps. The derivative has been correctly calculated.

Find the derivative of the following function. $\newline$ $y=\log _{2}\left(-9 x^{3}\right)$ $\newline$ Answer: $y^{\prime}=$

Full solution

More problems from Find derivatives of logarithmic functions

Related topics

Find the derivative of the following function.\newliney=log⁡2(−9x3) y=\log _{2}\left(-9 x^{3}\right) y=log2​(−9x3)\newlineAnswer: y′= y^{\prime}= y′=

Find the derivative of the following function. $\newline$ $y=\log _{2}\left(-9 x^{3}\right)$ $\newline$ Answer: $y^{\prime}=$