Full solution
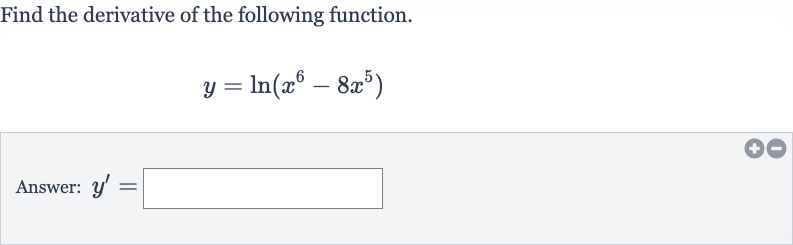
Q. Find the derivative of the following function.Answer:
- Identify Function Components: Identify the function and its components.We have . The function inside the natural logarithm is .
- Find Inner Function Derivative: Find the derivative of the inner function . Using the power rule, we differentiate term by term.
- Apply Chain Rule: Apply the chain rule to differentiate . The chain rule states that if , then . We already found in Step , and is given by the inner function.