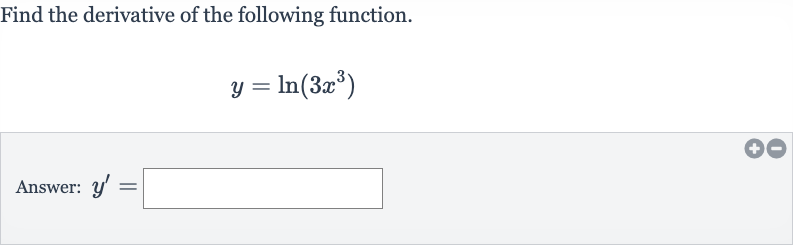
Find the derivative of the following function. y=ln(3x^(3)) Answer: y^(')=

Question

Find the derivative of the following function.  y=ln(3x^(3)) Answer:  y^(')=

Bytelearn · Accepted Answer

Identify Function Components: Identify the function and its components. The function y = ln(3x^(3)) can be rewritten as y = ln(3) + ln(x^(3)) by using the property of logarithms that ln(ab) = ln(a) + ln(b).Differentiate Constant Term: Differentiate the constant term ln(3). The derivative of a constant is 0, so the derivative of ln(3) is 0.Differentiate ln(x^(3)): Differentiate the term ln(x^(3)). Using the chain rule, the derivative of ln(u) with respect to x is 1/u * du/dx, where u = x^(3).Find Derivative of u: Find the derivative of u = x^(3). The derivative of x^(3) with respect to x is 3x^(2).Apply Chain Rule: Apply the chain rule to find the derivative of ln(x^(3)). The derivative of ln(x^(3)) is 1/(x^(3)) * 3x^(2).Simplify Derivative: Simplify the derivative. The derivative of ln(x^(3)) simplifies to 3x^(2)/(x^(3)) which further simplifies to 3/x.Combine Derivatives: Combine the derivatives of the constant term and the variable term. Since the derivative of ln(3) is 0, the derivative of the entire function y = ln(3x^(3)) is just the derivative of ln(x^(3)), which is 3/x.

Find the derivative of the following function. $\newline$ $y=\ln \left(3 x^{3}\right)$ $\newline$ Answer: $y^{\prime}=$

Full solution

More problems from Find derivatives of radical functions

Related topics

Find the derivative of the following function.\newliney=ln⁡(3x3) y=\ln \left(3 x^{3}\right) y=ln(3x3)\newlineAnswer: y′= y^{\prime}= y′=

Find the derivative of the following function. $\newline$ $y=\ln \left(3 x^{3}\right)$ $\newline$ Answer: $y^{\prime}=$