Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the derivative of the following function.

y=7^(-x^(4))
Answer:
y^(')=

Find the derivative of the following function. $\newline$ $y=7^{-x^{4}}$ $\newline$ Answer: $y^{\prime}=$

View step-by-step help

View step-by-step help

Find derivatives of radical functions

Full solution

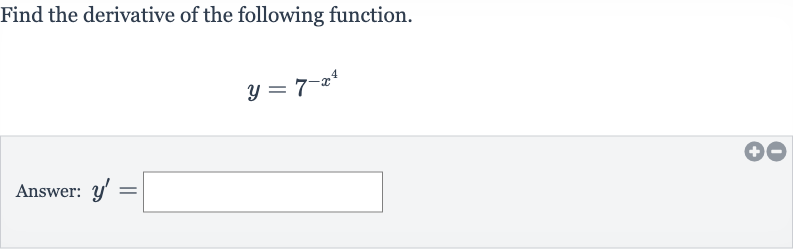
Q. Find the derivative of the following function.

\newline

y=7^{-x^{4}}

\newline

Answer:

y^{\prime}=

Given Function: We are given the function $y=7^{-x^{4}}$ . To find the derivative, we will use the chain rule and the exponential rule for derivatives.
Rewriting with Natural Log: Let's rewrite the function using the natural logarithm to make the differentiation easier. We can express $7$ as $e^{(\ln(7))}$ , so the function becomes $y = (e^{(\ln(7))})^{(-x^{4})}$ .
Apply Chain Rule: Now, apply the chain rule. The outer function is $e^{u}$ where $u = \ln(7)\cdot(-x^{4})$ , and the inner function is $u = \ln(7)\cdot(-x^{4})$ . We need to find the derivative of the outer function with respect to $u$ , and then multiply it by the derivative of $u$ with respect to $x$ .
Derivative of Outer Function: The derivative of $e^{u}$ with respect to $u$ is $e^{u}$ . So the derivative of the outer function with respect to $u$ is $e^{\ln(7)\cdot(-x^{4})}$ .
Derivative of Inner Function: Now, we differentiate the inner function $u = \ln(7)\cdot(-x^{4})$ with respect to $x$ . The constant $\ln(7)$ remains as it is, and the derivative of $-x^{4}$ with respect to $x$ is $-4x^{4-1}$ or $-4x^3$ .
Multiply Derivatives: Multiplying the derivative of the outer function by the derivative of the inner function, we get the derivative of $y$ with respect to $x$ : $\frac{dy}{dx} = e^{(\ln(7)\cdot(-x^{4}))} \cdot \ln(7) \cdot (-4x^{3})$ .
Simplify Expression: We can simplify the expression by remembering that $e^{\ln(7)}$ is just $7$ . So the derivative of $y$ with respect to $x$ is $\frac{dy}{dx} = 7^{-x^{4}} \cdot \ln(7) \cdot (-4x^{3})$ .
Final Derivative: Finally, we can write the derivative in its simplest form: $y' = -4 \cdot \ln(7) \cdot x^3 \cdot 7^{-x^{4}}$ .

More problems from Find derivatives of radical functions

Question

Find the derivative of

f(x)

\newline

f(x) = \cos(x)

\newline

f'(x) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \ln(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan^{-1}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = x e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \frac{e^x}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^{(x + 1)}

\newline

f'\left(x\right) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \sqrt{x+3}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

g(x)

\newline

g(x) = \ln(2x)

\newline

g^{\prime}(x) =

Posted 3 months ago