Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the derivative of the following function.

y=7^(6x^(6)-5x^(5))
Answer:
y^(')=

Find the derivative of the following function. $\newline$ $y=7^{6 x^{6}-5 x^{5}}$ $\newline$ Answer: $y^{\prime}=$

View step-by-step help

View step-by-step help

Find derivatives of radical functions

Full solution

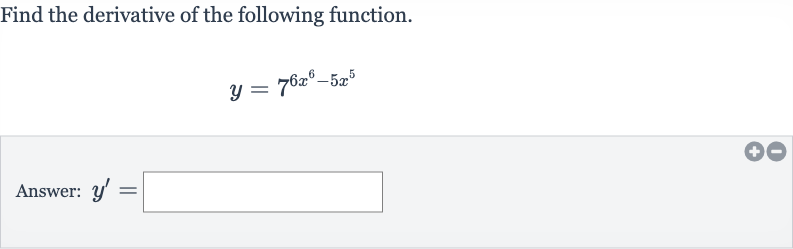
Q. Find the derivative of the following function.

\newline

y=7^{6 x^{6}-5 x^{5}}

\newline

Answer:

y^{\prime}=

Identify function components: Identify the function and its components. $\newline$ The function is $y = 7^{6x^6 - 5x^5}$ , which is an exponential function with a base of $7$ and an exponent of $6x^6 - 5x^5$ .
Use chain rule for differentiation: Recognize that to differentiate $y = 7^{6x^6 - 5x^5}$ , we need to use the chain rule for exponential functions. $\newline$ The chain rule states that the derivative of $a^u$ , where $a$ is a constant and $u$ is a function of $x$ , is $a^u \cdot \ln(a) \cdot u'$ .
Differentiate exponent function: Differentiate the exponent function $u(x) = 6x^6 - 5x^5$ . To find $u'(x)$ , we apply the power rule to each term. $u'(x) = \frac{d}{dx}(6x^6) - \frac{d}{dx}(5x^5)$ $u'(x) = 36x^5 - 25x^4$
Apply chain rule to find derivative: Apply the chain rule to find the derivative of $y$ . Using the chain rule, we get $y' = 7^{(6x^6 - 5x^5)} \cdot \ln(7) \cdot (36x^5 - 25x^4)$ .
Simplify derivative expression: Simplify the expression for the derivative. $\newline$ $y' = (7^{6x^6 - 5x^5}) \cdot \ln(7) \cdot (36x^5 - 25x^4)$ $\newline$ This is the final form of the derivative.

More problems from Find derivatives of radical functions

Question

Find the derivative of

f(x)

\newline

f(x) = \cos(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan(x)

\newline

f'(x) =

Posted 3 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^x

\newline

f'\left(x\right) =

Posted 3 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \ln(x)

\newline

f'(x) =

Posted 3 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan^{-1}{x}

\newline

f'(x) =

Posted 3 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = x e^x

\newline

f'\left(x\right) =

Posted 3 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \frac{e^x}{x}

\newline

f'(x) =

Posted 3 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^{(x + 1)}

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \sqrt{x+3}

\newline

f'(x) =

Posted 3 months ago

Question

Find the derivative of

g(x)

\newline

g(x) = \ln(2x)

\newline

g^{\prime}(x) =

Posted 4 months ago