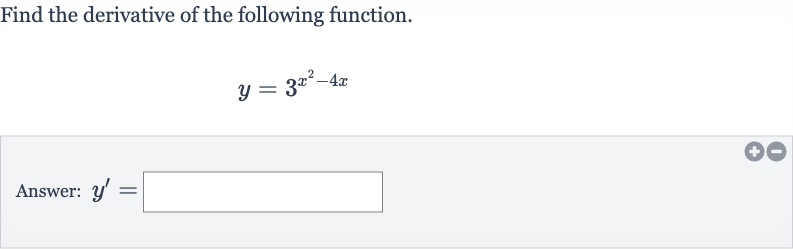
Find the derivative of the following function. y=3^(x^(2)-4x) Answer: y^(')=

Question

Find the derivative of the following function.  y=3^(x^(2)-4x) Answer:  y^(')=

Bytelearn · Accepted Answer

Identify function components: Identify the function and its components. The function y = 3^(x^2 - 4x) is an exponential function with base 3 and exponent x^2 - 4x.Apply chain rule for derivatives: Apply the chain rule for derivatives. The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. In this case, the outer function is 3^u and the inner function is u(x) = x^2 - 4x.Find derivative of outer function: Find the derivative of the outer function with respect to u. The derivative of 3^u with respect to u is 3^u * ln(3), where ln(3) is the natural logarithm of 3.Find derivative of inner function: Find the derivative of the inner function with respect to x. The derivative of u(x) = x^2 - 4x with respect to x is d/dx(x^2) - d/dx(4x), which simplifies to 2x - 4.Apply chain rule: Apply the chain rule. Using the chain rule, the derivative of y with respect to x is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. This gives us y' = (3^(x^2 - 4x) * ln(3)) * (2x - 4).Simplify expression: Simplify the expression. We can simplify the expression for the derivative to y' = 3^(x^2 - 4x) * ln(3) * (2x - 4).

Find the derivative of the following function. $\newline$ $y=3^{x^{2}-4 x}$ $\newline$ Answer: $y^{\prime}=$

Full solution

More problems from Find derivatives of radical functions

Related topics

Find the derivative of the following function.\newliney=3x2−4x y=3^{x^{2}-4 x} y=3x2−4x\newlineAnswer: y′= y^{\prime}= y′=

Find the derivative of the following function. $\newline$ $y=3^{x^{2}-4 x}$ $\newline$ Answer: $y^{\prime}=$