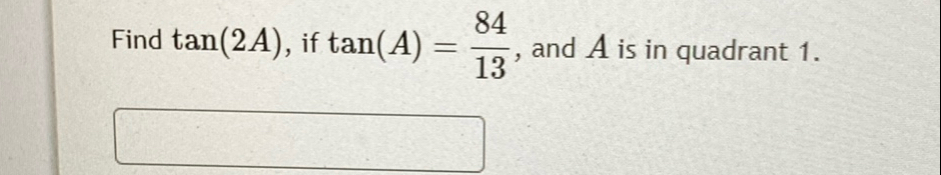Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find tan(2A), if tan(A)=(84)/(13), and A is in quadrant 1.

Find tan⁡(2A) \tan (2 A) , if tan⁡(A)=8413 \tan (A)=\frac{84}{13} , and A A is in quadrant 11.

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Quadrantsright chevron icon

Full solution

Q. Find tan⁡(2A) \tan (2 A) , if tan⁡(A)=8413 \tan (A)=\frac{84}{13} , and A A is in quadrant 11.
  1. Apply double angle formula: Use the double angle formula for tangent, which is tan⁡(2A)=2tan⁡(A)1−tan⁡2(A)\tan(2A) = \frac{2\tan(A)}{1 - \tan^2(A)}.\newlineCalculation: tan⁡(2A)=2×(8413)1−(8413)2.\tan(2A) = \frac{2 \times (\frac{84}{13})}{1 - (\frac{84}{13})^2}.
  2. Simplify expression: Simplify the expression for tan⁡(2A)\tan(2A).\newlineCalculation: tan⁡(2A)=2×(8413)1−(7056169)\tan(2A) = \frac{2 \times (\frac{84}{13})}{1 - (\frac{7056}{169})}.
  3. Calculate denominator: Continue simplifying by calculating the denominator.\newlineCalculation: 1−(7056169)=(169169)−(7056169)=−68871691 - \left(\frac{7056}{169}\right) = \left(\frac{169}{169}\right) - \left(\frac{7056}{169}\right) = \frac{-6887}{169}.
  4. Calculate tan⁡(2A)\tan(2A): Calculate tan⁡(2A)\tan(2A) with the simplified denominator.\newlineCalculation: tan⁡(2A)=16813/−6887169=16813⋅−1696887\tan(2A) = \frac{168}{13} / \frac{-6887}{169} = \frac{168}{13} \cdot \frac{-169}{6887}.
  5. Simplify multiplication: Simplify the multiplication.\newlineCalculation: tan⁡(2A)=−168×169/(13×6887)\tan(2A) = -168 \times 169 / (13 \times 6887).
  6. Perform final calculation: Perform the final calculation.\newlineCalculation: tan⁡(2A)=−2845289471\tan(2A) = -\frac{28452}{89471}.

More problems from Quadrants

Question
Find the measure of a negative angle coterminal with 180∘180^\circ. \newline____∘^\circ
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the measure of the reference angle for a 170∘170^\circ angle.
Get tutor helpright-arrow

Posted 1 month ago

Question
How many radians is 60∘60^\circ?\newlineChoices: \newline[A]π3 radians[A]\frac{\pi}{3}\text{ radians}\newline[B]π2 radians[B]\frac{\pi}{2}\text{ radians}\newline[C]π4 radians[C]\frac{\pi}{4}\text{ radians}\newline[D]π6 radians[D]\frac{\pi}{6}\text{ radians}
Get tutor helpright-arrow

Posted 2 months ago

Question
Which of the following radian measures is equal to 90∘ 90^{\circ} ?\newlineChoose 11 answer:\newline(A) π3 \frac{\pi}{3} radians\newlineB π4 \frac{\pi}{4} radians\newline(C) π2 \frac{\pi}{2} radians\newline(D) π6 \frac{\pi}{6} radians
Get tutor helpright-arrow

Posted 2 months ago

Question
Which of the following radian measures is equal to 225∘ 225^{\circ} ?\newlineChoose 11 answer:\newline(A) π4 \frac{\pi}{4} radians\newlineB π2 \frac{\pi}{2} radians\newline(C) 3π4 \frac{3 \pi}{4} radians\newline(D) 5π4 \frac{5 \pi}{4} radians
Get tutor helpright-arrow

Posted 4 months ago

Question
Which of the following radian measures is equal to 135∘ 135^{\circ} ?\newlineChoose 11 answer:\newline(A) π4 \frac{\pi}{4} radians\newline(B) π2 \frac{\pi}{2} radians\newline(C) 3π4 \frac{3 \pi}{4} radians\newline(D) π \pi radians
Get tutor helpright-arrow

Posted 4 months ago

Question
Which of the following radian measures is equal to 330∘ 330^{\circ} ?\newlineChoose 11 answer:\newline(A) 15π6 \frac{15 \pi}{6} radians\newlineB 7π6 \frac{7 \pi}{6} radians\newline(C) 11π6 \frac{11 \pi}{6} radians\newline(D) 13π6 \frac{13 \pi}{6} radians
Get tutor helpright-arrow

Posted 4 months ago

Question
Which of the following radian measures is equal to 75∘ 75^{\circ} ?\newlineChoose 11 answer:\newline(A) π12 \frac{\pi}{12} radians\newlineB π3 \frac{\pi}{3} radians\newline(C) 5π12 \frac{5 \pi}{12} radians\newline(D) 7π12 \frac{7 \pi}{12} radians
Get tutor helpright-arrow

Posted 2 months ago

Question
Which of the following radian measures is equal to 240∘ 240^{\circ} ?\newlineChoose 11 answer:\newline(A) 4π3 \frac{4 \pi}{3} radians\newlineB 5π3 \frac{5 \pi}{3} radians\newline(C) 7π3 \frac{7 \pi}{3} radians\newline(D) 11π3 \frac{11 \pi}{3} radians
Get tutor helpright-arrow

Posted 4 months ago

Question
Which of the following radian measures is equal to 120∘ 120^{\circ} ?\newlineChoose 11 answer:\newline(A) 2π3 \frac{2 \pi}{3} radians\newline(B) π \pi radians\newline(C) 4π3 \frac{4 \pi}{3} radians\newline(D) 5π3 \frac{5 \pi}{3} radians
Get tutor helpright-arrow

Posted 4 months ago

View all (30)