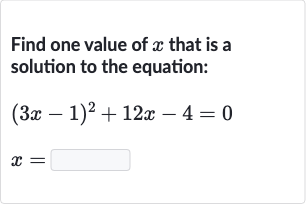Full solution
Q. Find one value of that is a solution to the equation:
- Expand squared term: First, let's expand the squared term .
- Substitute expanded term: Now, substitute the expanded term back into the original equation.
- Combine like terms: Combine like terms.
- Solve using quadratic formula: This is a quadratic equation, and we can solve for by factoring, completing the square, or using the quadratic formula. The equation does not factor easily, so let's use the quadratic formula: , where , , and .
- Calculate discriminant: First, calculate the discriminant .Discriminant =
- Apply quadratic formula: Since the discriminant is positive, there are two real solutions. Now, apply the quadratic formula.
- Calculate possible values: Calculate the two possible values for .
More problems from Solve linear equations: mixed review
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help