AI tutor
Full solution
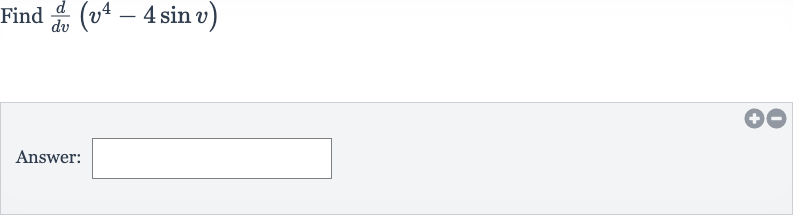
Q. Find Answer:
- Apply Power Rule: Differentiate the function term by term.The function we are differentiating is . We will apply the power rule to the first term and the derivative of the sine function to the second term.
- Power Rule for : Apply the power rule to the first term . The power rule states that . Therefore, the derivative of with respect to is: $(\frac{d}{dv})(v^{\(4\)}) = \(4\)v^{\(4\)\(-1\)} = \(4\)v^\(3\).
- Differentiate \(-4\sin(v)\): Differentiate the second term \(-4\sin(v)\). The derivative of \(\sin(v)\) with respect to \(v\) is \(\cos(v)\). Therefore, the derivative of \(-4\sin(v)\) with respect to \(v\) is: \((\frac{d}{dv})(-4\sin(v)) = -4\cos(v)\).
- Combine Derivatives: Combine the derivatives of the individual terms.\(\newline\)The derivative of the entire function \(v^{4}-4\sin(v)\) with respect to \(v\) is the sum of the derivatives of its terms:\(\newline\)\(\frac{d}{dv}(v^{4}-4\sin(v)) = 4v^3 - 4\cos(v)\).