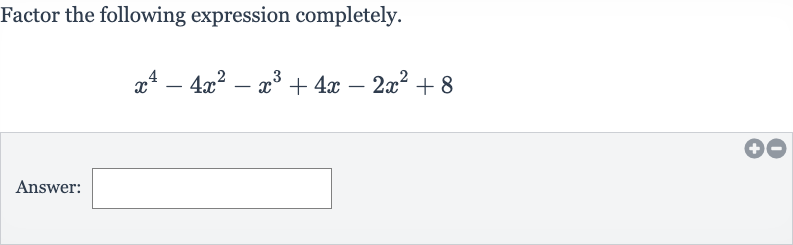
Factor the following expression completely. x^(4)-4x^(2)-x^(3)+4x-2x^(2)+8 Answer:

Question

Factor the following expression completely.  x^(4)-4x^(2)-x^(3)+4x-2x^(2)+8 Answer:

Bytelearn · Accepted Answer

Rewrite in Descending Order: First, let's rewrite the expression in descending order of the powers of x: x^(4) - x^(3) - 4x^(2) - 2x^(2) + 4x + 8 Now, combine like terms: x^(4) - x^(3) - 6x^(2) + 4x + 8Combine Like Terms: Next, we look for common factors or patterns that might help us factor the expression. We can try to group terms to see if that helps: (x^(4) - x^(3)) - (6x^(2) - 4x) + 8 Now, factor out the common x^3 from the first group and 2x from the second group: x^3(x - 1) - 2x(3x - 2) + 8Factor Out Common Factors: At this point, we notice that there is no common factor that we can factor out from all terms, and the expression does not fit any special factoring formulas (such as difference of squares or sum/difference of cubes). We can try to factor by grouping, but we need to rearrange or combine terms in a way that might reveal a factorable pattern. Let's try to factor by grouping in pairs: (x^3(x - 1) - 2x(3x - 2)) + 8 However, this does not seem to lead to a factorable expression. We may need to try a different approach or check if the expression is factorable at all.Factor by Grouping: Let's try a different grouping that might reveal a factorable pattern: (x^4 - 6x^2 + 8) - (x^3 - 4x) Now, we look for a common factor or pattern in each group. The first group resembles a quadratic trinomial, and the second group has a common factor of x: (x^2)^2 - 2*(3x^2) + 2^2 - x(x^2 - 4) The first group is a perfect square trinomial, and the second group has a difference of squares: (x^2 - 2)^2 - x(x + 2)(x - 2)Try Different Grouping: Now, we have a difference of squares in the second group, which we already factored, and a perfect square trinomial in the first group. We can write the expression as: (x^2 - 2)^2 - x(x + 2)(x - 2) This is the factored form of the expression, as we cannot factor it further.

Factor the following expression completely. $\newline$ $x^{4}-4 x^{2}-x^{3}+4 x-2 x^{2}+8$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor the following expression completely.\newlinex4−4x2−x3+4x−2x2+8 x^{4}-4 x^{2}-x^{3}+4 x-2 x^{2}+8 x4−4x2−x3+4x−2x2+8\newlineAnswer:

Factor the following expression completely. $\newline$ $x^{4}-4 x^{2}-x^{3}+4 x-2 x^{2}+8$ $\newline$ Answer: