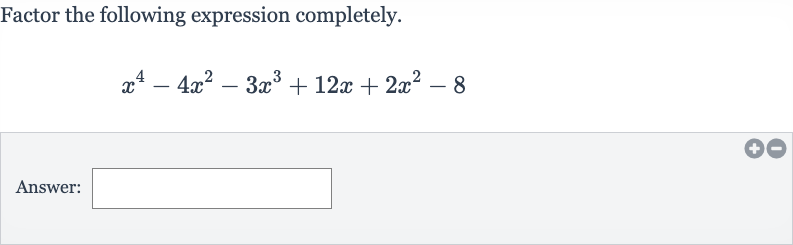
Factor the following expression completely. x^(4)-4x^(2)-3x^(3)+12 x+2x^(2)-8 Answer:

Question

Factor the following expression completely.  x^(4)-4x^(2)-3x^(3)+12 x+2x^(2)-8 Answer:

Bytelearn · Accepted Answer

Rearrange and Combine Terms: First, we should rearrange the terms of the polynomial in descending order of the powers of x. x^(4) - 3x^(3) - 4x^(2) + 2x^(2) + 12x - 8 Now, combine like terms. x^(4) - 3x^(3) - 2x^(2) + 12x - 8Factor Out Common Factors: Next, we look for common factors in groups of terms. We can group the terms as follows: (x^(4) - 3x^(3)) + (-2x^(2) + 12x) - 8 Now, factor out the greatest common factor from each group. x^(3)(x - 3) - 2x(x - 6) - 8Explore Different Grouping: We notice that there is no common factor that we can factor out from all terms. However, we can look for a pattern or try to factor by grouping in a different way. Let's try to factor by grouping in pairs differently: (x^(4) - 4x^(2)) - (3x^(3) - 12x) + (2x^(2) - 8) Now, factor out the greatest common factor from each pair. x^(2)(x^(2) - 4) - 3x(x^(2) - 4) + 2(x^(2) - 4)Factor Quadratic: We can see that (x^(2) - 4) is a common factor in all three groups. Let's factor that out. (x^(2) - 4)(x^(2) - 3x + 2)Factor Difference of Squares: Now, we need to factor the quadratic x^(2) - 3x + 2. This is a simple quadratic that can be factored into two binomials. (x - 1)(x - 2)Combine All Factors: The factor (x^(2) - 4) is a difference of squares, which can be factored further. (x + 2)(x - 2)Final Factored Expression: Now, we combine all the factors we have found to write the completely factored expression. (x + 2)(x - 2)(x - 1)(x - 2)We notice that (x - 2) appears twice, so we can write it as a square. (x + 2)(x - 2)^2(x - 1) This is the completely factored form of the given expression.

Factor the following expression completely. $\newline$ $x^{4}-4 x^{2}-3 x^{3}+12 x+2 x^{2}-8$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor the following expression completely.\newlinex4−4x2−3x3+12x+2x2−8 x^{4}-4 x^{2}-3 x^{3}+12 x+2 x^{2}-8 x4−4x2−3x3+12x+2x2−8\newlineAnswer:

Factor the following expression completely. $\newline$ $x^{4}-4 x^{2}-3 x^{3}+12 x+2 x^{2}-8$ $\newline$ Answer: