Full solution
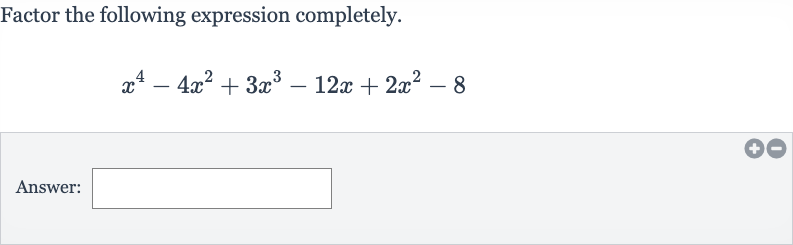
Q. Factor the following expression completely.Answer:
- Rearrange and Combine Terms: First, we should rearrange the terms in descending order of the powers of . Now, combine like terms.
- Look for Common Factors: Next, we look for common factors in groups of terms. We can group the terms as follows:Now, factor out the greatest common factor from each group.
- Factor Out Common Factors: We notice that there is no common factor that we can factor out from all terms. However, we can try to factor by grouping. Let's rearrange the terms to see if we can group them differently:Now, let's factor the quadratic expression in the second group.