AI tutor
Full solution
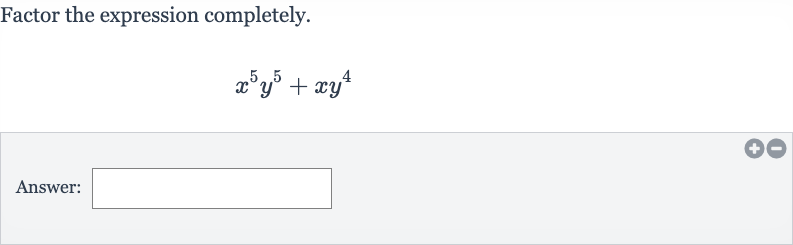
Q. Factor the expression completely.Answer:
- Identify GCF: Identify the greatest common factor (GCF) of the terms in the expression and . The GCF is because it is the highest degree of and that divides both terms.
- Factor out GCF: Factor out the GCF from the expression.We divide each term by to find the remaining factors.
- Divide terms: Check the factored expression to ensure that when the GCF is distributed back into the parentheses, we get the original expression.The original expression is obtained, so there is no math error.