AI tutor
Full solution
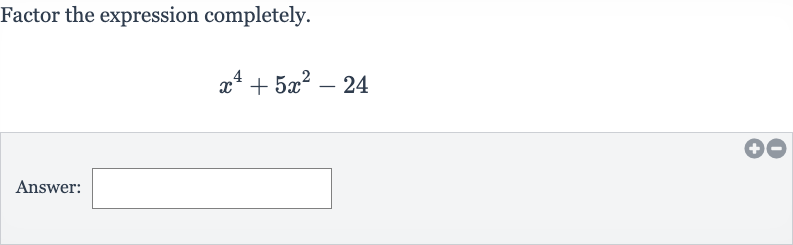
Q. Factor the expression completely.Answer:
- Recognize Quadratic Form: Recognize the expression as a quadratic in form.The given expression can be treated as a quadratic equation if we let . This gives us .
- Factor Quadratic Expression: Factor the quadratic expression.We need to find two numbers that multiply to and add up to . These numbers are and . So we can write as .
- Substitute Back : Substitute back for .Now we replace with to get the factors in terms of : .
- Check Further Factoring: Check if the factors can be factored further.The term cannot be factored further over the real numbers because it does not correspond to the difference of squares and does not have real roots. The term is already in its simplest form as the difference of squares. Therefore, the expression is fully factored.