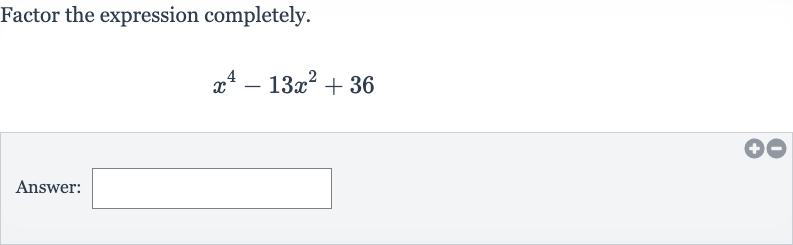
Factor the expression completely. x^(4)-13x^(2)+36 Answer:

Question

Factor the expression completely.  x^(4)-13x^(2)+36 Answer:

Bytelearn · Accepted Answer

Identify Quadratic Form: We are asked to factor the expression x^4 - 13x^2 + 36. This is a quadratic in form, where the variable x^2 is taking the place of x in a standard quadratic equation. We will look for two numbers that multiply to 36 and add up to -13.Find Factor Pairs: Let's set up the factors of 36 and find the pair that adds up to -13. The pairs of factors of 36 are (1, 36), (2, 18), (3, 12), (4, 9), (6, 6). We notice that the pair (4, 9) can add up to -13 if both are negative: -4 and -9.Write Factored Quadratic: Now we can write the expression as a factored quadratic: x^4 - 13x^2 + 36 = (x^2 - 4)(x^2 - 9). We have factored the original expression into the product of two binomials.Factor Differences of Squares: We notice that both binomials are differences of squares. The difference of squares can be factored further as (a^2 - b^2) = (a - b)(a + b). We apply this to both binomials.Factor x^2 - 4: First, we factor x^2 - 4 as (x - 2)(x + 2). This is because 4 is 2^2, and we apply the difference of squares formula.Factor x^2 - 9: Next, we factor x^2 - 9 as (x - 3)(x + 3). This is because 9 is 3^2, and we again apply the difference of squares formula.Combine Factors: Combining the factors from the previous two steps, we get the complete factorization of the original expression: x^4 - 13x^2 + 36 = (x - 2)(x + 2)(x - 3)(x + 3).

Factor the expression completely. $\newline$ $x^{4}-13 x^{2}+36$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor the expression completely.\newlinex4−13x2+36 x^{4}-13 x^{2}+36 x4−13x2+36\newlineAnswer:

Factor the expression completely. $\newline$ $x^{4}-13 x^{2}+36$ $\newline$ Answer: