AI tutor
Full solution
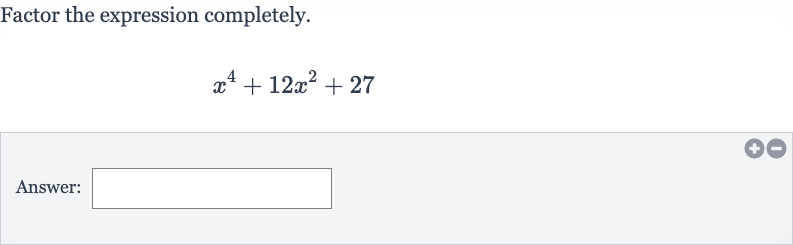
Q. Factor the expression completely.Answer:
- Identify Type and Patterns: Identify the type of polynomial and look for patterns. The given expression is a quadratic in form, with taking the place of in a standard quadratic equation. We can substitute to make it look like a standard quadratic equation: .
- Factor the Quadratic Expression: Factor the quadratic expression.We need to find two numbers that multiply to and add up to . These numbers are and .So, we can write as .
- Substitute Back : Substitute back for . Replace with in the factored form to get .
- Check for Further Factoring: Check if further factoring is possible.The terms and cannot be factored further over the real numbers because they do not have real roots. Therefore, the expression is fully factored.