AI tutor
Full solution
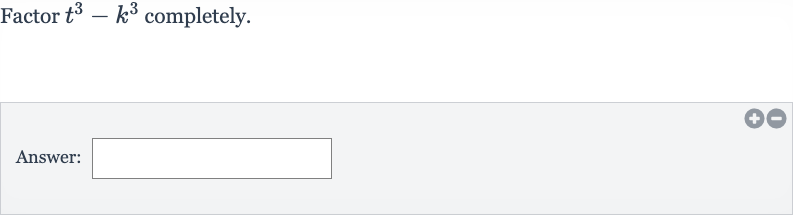
Q. Factor completely.Answer:
- Use Difference of Cubes Formula: To factor the difference of cubes , we use the formula , where and .
- Apply the Formula: Applying the formula, we get: .
- Check for Common Factors: We check for any common factors in the terms , , and . There are none, so the factorization is complete.
- Final Answer: The final answer is the factorization of , which is .