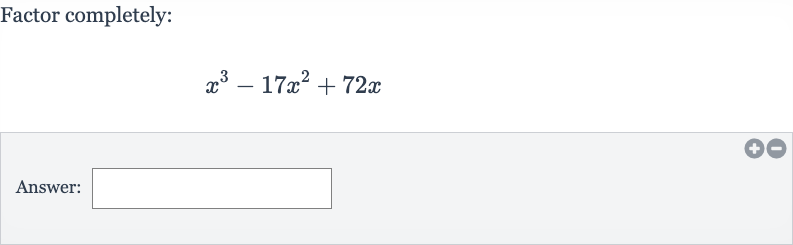AI tutor
Full solution
Q. Factor completely:Answer:
- Identify common factors: Identify common factors in all terms of the polynomial . All terms have an in common, so we can factor out .
- Factor quadratic expression: Factor the quadratic expression . We need to find two numbers that multiply to and add up to . These numbers are and .
- Check factored form: Check the factored form by expanding it to ensure it matches the original polynomial. The expanded form matches the original polynomial, so the factoring is correct.