AI tutor
Full solution
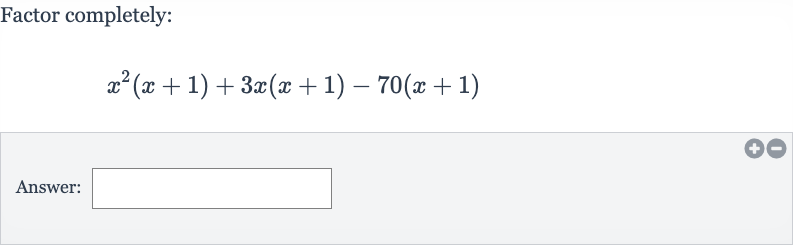
Q. Factor completely:Answer:
- Factor out common term: First, notice that each term in the expression contains a common factor of . We can factor out from each term.
- Factor quadratic expression: Now we need to factor the quadratic expression . We look for two numbers that multiply to and add up to . These numbers are and .
- Combine factored parts: We can now write the completely factored form of the original expression by combining the factored parts.