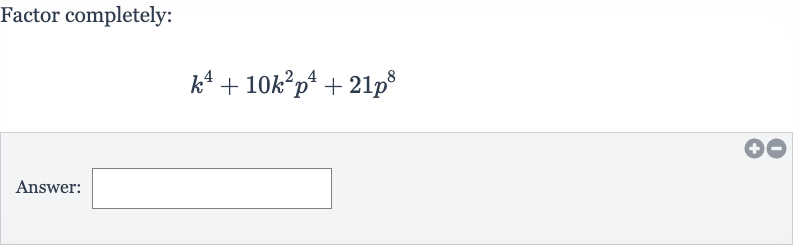Factor completely: k^(4)+10k^(2)p^(4)+21p^(8) Answer:

Question

Factor completely:  k^(4)+10k^(2)p^(4)+21p^(8) Answer:

Bytelearn · Accepted Answer

Recognize Structure: Recognize the structure of the expression. The given expression k^(4)+10k^(2)p^(4)+21p^(8) resembles a quadratic in form, where k^(2) plays the role of 'x' and p^(4) plays the role of 'y'. So, we can think of this as factoring a quadratic trinomial of the form x^2 + bx + c.Find Factors: Look for factors of the constant term that add up to the coefficient of the middle term. We need to find two numbers that multiply to 21p^(8) and add up to 10k^(2). The numbers that satisfy this are 3p^(4) and 7p^(4) because 3p^(4) * 7p^(4) = 21p^(8) and 3p^(4) + 7p^(4) = 10p^(4).Write Trinomial: Write the expression as a quadratic trinomial and factor it. We can rewrite the expression as (k^(2) + 3p^(4))(k^(2) + 7p^(4)) by grouping the terms that we found in the previous step.Check Factored Form: Check the factored form by expanding it to ensure it matches the original expression. Expanding (k^(2) + 3p^(4))(k^(2) + 7p^(4)), we get k^(4) + 3p^(4)k^(2) + 7p^(4)k^(2) + 21p^(8), which simplifies to k^(4) + 10k^(2)p^(4) + 21p^(8), matching the original expression.Write Final Answer: Write the final answer. The complete factorization of the expression k^(4)+10k^(2)p^(4)+21p^(8) is (k^(2) + 3p^(4))(k^(2) + 7p^(4)).

Factor completely: $\newline$ $k^{4}+10 k^{2} p^{4}+21 p^{8}$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor completely:\newlinek4+10k2p4+21p8 k^{4}+10 k^{2} p^{4}+21 p^{8} k4+10k2p4+21p8\newlineAnswer:

Factor completely: $\newline$ $k^{4}+10 k^{2} p^{4}+21 p^{8}$ $\newline$ Answer: