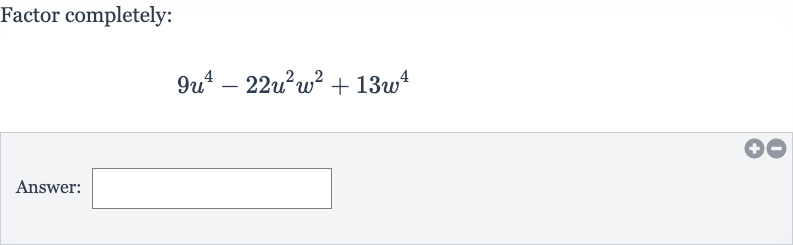
Factor completely: 9u^(4)-22u^(2)w^(2)+13w^(4) Answer:

Question

Factor completely:  9u^(4)-22u^(2)w^(2)+13w^(4) Answer:

Bytelearn · Accepted Answer

Identify Quadratic Form: Identify the polynomial as a quadratic in form with respect to u^2. The polynomial 9u^(4)-22u^(2)w^(2)+13w^(4) can be treated as a quadratic in u^2, where u^2 is the variable and 9, -22w^2, and 13w^4 are the coefficients.Find Multiplying Numbers: Look for two numbers that multiply to 9*13w^4 and add to -22w^2. We need to find two numbers that when multiplied give us 9*13w^4 = 117w^4 and when added give us -22w^2. These numbers are -9w^2 and -13w^2.Write Four-Term Expression: Write the polynomial as a four-term expression using the numbers found. We can express the polynomial as 9u^(4) - 9u^2w^2 - 13u^2w^2 + 13w^4.Factor by Grouping: Factor by grouping. We group the terms as (9u^(4) - 9u^2w^2) and (-13u^2w^2 + 13w^4) and factor out the common factors from each group.Factor Common Factors: Factor out the common factors from each group. From the first group (9u^(4) - 9u^2w^2), we factor out 9u^2, and from the second group (-13u^2w^2 + 13w^4), we factor out -13w^2. This gives us 9u^2(u^2 - w^2) - 13w^2(u^2 - w^2).Factor Common Binomial: Factor out the common binomial factor. We notice that (u^2 - w^2) is a common factor in both terms, so we factor it out to get (u^2 - w^2)(9u^2 - 13w^2).Recognize Difference of Squares: Recognize that u^2 - w^2 is a difference of squares. The expression u^2 - w^2 is a difference of squares and can be factored further into (u + w)(u - w).Write Final Factorization: Write the final factorization. The complete factorization of the polynomial is (u + w)(u - w)(9u^2 - 13w^2).

Factor completely: $\newline$ $9 u^{4}-22 u^{2} w^{2}+13 w^{4}$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor completely:\newline9u4−22u2w2+13w4 9 u^{4}-22 u^{2} w^{2}+13 w^{4} 9u4−22u2w2+13w4\newlineAnswer:

Factor completely: $\newline$ $9 u^{4}-22 u^{2} w^{2}+13 w^{4}$ $\newline$ Answer: