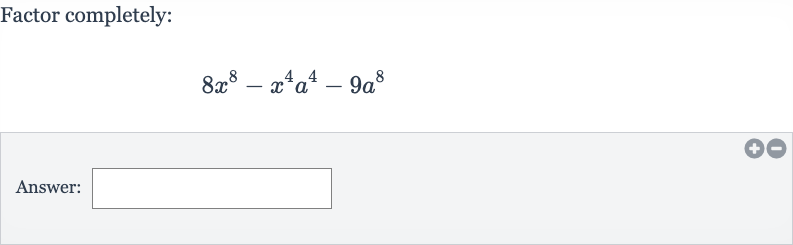AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Factor completely:Answer:
Full solution
Q. Factor completely:Answer:
- Identify Factoring Technique: We are looking to factor the polynomial . To start, we can try to identify a common pattern or structure in the polynomial that might suggest a particular factoring technique. One technique that might be useful here is factoring by grouping, since we have three terms. We can also look for a common factor in all terms, but there is none in this case. Let's proceed with factoring by grouping.
- Grouping Terms: We can group the terms as follows: - . Now we will look for common factors within each group. The first group has a common factor of , and the second group is a single term which is a perfect square.
- Factor Out Common Factor: Factoring out the common factor of from the first group gives us . The second group is already a perfect square, , which can be written as . Now our expression looks like this: .
- Apply Difference of Squares: We notice that the expression inside the parentheses, , is a difference of squares since is and is . The difference of squares can be factored as . Applying this to , we get .
- Correct Error: Now we substitute back into our expression with the factored form of . We get . However, we made a mistake in the previous step; we did not correctly apply the difference of squares to the term . The correct factorization of should be , which is already in the factored form as a difference of squares. We need to correct this error.
