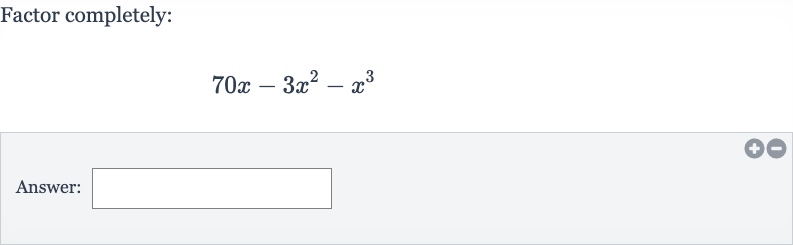Factor completely: 70 x-3x^(2)-x^(3) Answer:

Question

Factor completely:  70 x-3x^(2)-x^(3) Answer:

Bytelearn · Accepted Answer

Recognize common factor: First, we need to recognize that each term in the polynomial 70x - 3x^2 - x^3 has a common factor of x. We can factor out the greatest common factor (GCF) from each term.Factor out GCF: Factor out the GCF, which is x: x(70 - 3x - x^2) Now we have factored out x, but we need to check if the remaining quadratic polynomial can be factored further.Check quadratic polynomial: We should rearrange the terms in the quadratic polynomial to have them in standard form (from highest power to lowest power): x(-x^2 - 3x + 70)Rearrange terms in standard form: Now, we look for two numbers that multiply to give the product of the coefficient of x^2 (-1) and the constant term (70), and add up to the coefficient of x (-3). The numbers that satisfy these conditions are -10 and 7, because (-10) * 7 = -70 and (-10) + 7 = -3.Find two numbers: We can now factor the quadratic polynomial using these two numbers: x(-x^2 - 10x + 7x + 70)Factor quadratic polynomial: Next, we group the terms to factor by grouping: x((-x^2 - 10x) + (7x + 70))Group terms for factoring: Factor out the common factors from each group: x(-x(x + 10) + 7(x + 10))Factor out common factors: We see that (x + 10) is a common factor in both groups, so we can factor it out: x(x + 10)(-x + 7)Write completely factored form: Finally, we can write the completely factored form of the polynomial: x(-x + 7)(x + 10) However, it is more conventional to write the factors in descending order of their powers of x: -x^3 - 3x^2 + 70x = -x(x - 7)(x + 10)

Factor completely: $\newline$ $70 x-3 x^{2}-x^{3}$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor completely:\newline70x−3x2−x3 70 x-3 x^{2}-x^{3} 70x−3x2−x3\newlineAnswer:

Factor completely: $\newline$ $70 x-3 x^{2}-x^{3}$ $\newline$ Answer: