AI tutor
Full solution
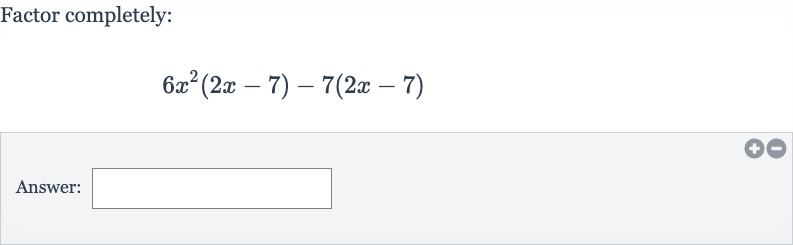
Q. Factor completely:Answer:
- Identify Common Factor: Identify the common factor in both terms.The expression is . Both terms have a common factor of .
- Factor Out Common Factor: Factor out the common factor . We can write the expression as .
- Check for Further Factoring: Check if the remaining terms can be factored further. The remaining terms inside the parentheses are and , which do not have any common factors other than , and is not a perfect square nor is . Therefore, the expression is fully factored.
- Write Final Answer: Write the final answer.The completely factored form of the expression is .
More problems from Powers with negative bases
QuestionGet tutor help