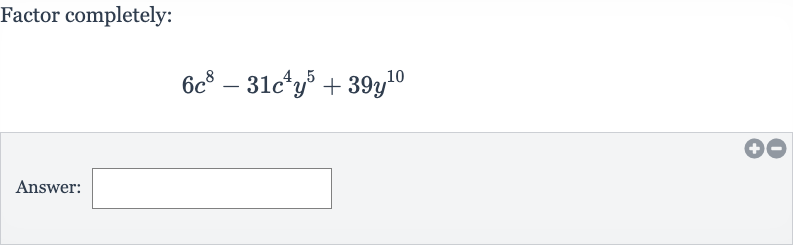Factor completely: 6c^(8)-31c^(4)y^(5)+39y^(10) Answer:

Question

Factor completely:  6c^(8)-31c^(4)y^(5)+39y^(10) Answer:

Bytelearn · Accepted Answer

Identify Polynomial Structure: Identify the structure of the polynomial. The given polynomial is a trinomial in the form of ax^2 + bx + c, where x is replaced by c^4 and a = 6, b = -31, and c = 39.Find Common Factor: Look for a common factor in all three terms. There is no common factor in all three terms, so we proceed to factor by grouping or other methods.Factor as Quadratic Equation: Since the polynomial is a quadratic in form with respect to c^4, we can try to factor it as if it were a quadratic equation. We look for two numbers that multiply to ac (6 * 39) and add to b (-31). We need to find two numbers that multiply to 234 (6 * 39) and add up to -31.Find Two Numbers: Find the two numbers that satisfy the conditions from Step 3. The numbers -26 and -5 satisfy these conditions because -26 * -5 = 130 and -26 + -5 = -31.Rewrite Middle Term: Rewrite the middle term of the polynomial using the two numbers found in Step 4. 6c^(8) - 26c^(4)y^(5) - 5c^(4)y^(5) + 39y^(10)Factor by Grouping: Factor by grouping. Group the first two terms together and the last two terms together. (6c^(8) - 26c^(4)y^(5)) - (5c^(4)y^(5) - 39y^(10))Factor Out Common Factor: Factor out the greatest common factor from each group. 2c^(4)(3c^(4) - 13y^(5)) - y^(5)(5c^(4) - 39y^(5))Identify Common Factor: Notice that (3c^(4) - 13y^(5)) is a common factor in both groups. 2c^(4)(3c^(4) - 13y^(5)) - y^(5)(3c^(4) - 13y^(5))Factor Out Common Factor: Factor out the common factor (3c^(4) - 13y^(5)). (3c^(4) - 13y^(5))(2c^(4) - y^(5))Write Final Factorized Form: Write down the final factorized form of the polynomial. The polynomial 6c^(8) - 31c^(4)y^(5) + 39y^(10) is completely factored as (3c^(4) - 13y^(5))(2c^(4) - y^(5)).

Factor completely: $\newline$ $6 c^{8}-31 c^{4} y^{5}+39 y^{10}$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor completely:\newline6c8−31c4y5+39y10 6 c^{8}-31 c^{4} y^{5}+39 y^{10} 6c8−31c4y5+39y10\newlineAnswer:

Factor completely: $\newline$ $6 c^{8}-31 c^{4} y^{5}+39 y^{10}$ $\newline$ Answer: