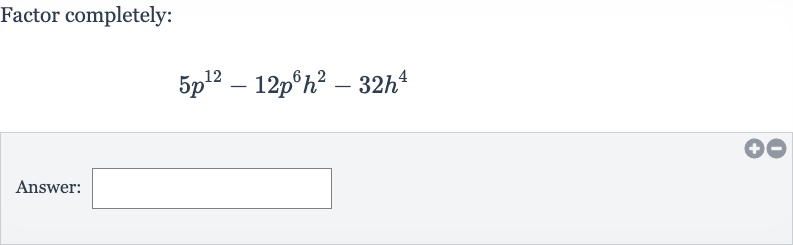
Factor completely: 5p^(12)-12p^(6)h^(2)-32h^(4) Answer:

Question

Factor completely:  5p^(12)-12p^(6)h^(2)-32h^(4) Answer:

Bytelearn · Accepted Answer

Identify Common Factors: First, we look for common factors in each term of the expression 5p^(12)-12p^(6)h^(2)-32h^(4). We can see that there are no common factors among all three terms.Attempt Grouping Factorization: Next, we can try to factor by grouping. To do this, we need to find a way to split the middle term or rearrange the terms to find a common factor. However, since there are no obvious groupings that will work, we move on to the next step.Explore Factoring Patterns: We can look for patterns that resemble known factoring formulas, such as the difference of squares or perfect square trinomials. However, this expression does not fit any of those patterns directly.Factor by Substitution: Since the expression is a trinomial and the terms involve p^(6) and h^(2), we can try to factor by substitution. Let's set q = p^(6) and r = h^(2), so the expression becomes 5q^2 - 12qr - 32r^2.Apply AC Method for Quadratic: Now we have a quadratic in terms of q and r: 5q^2 - 12qr - 32r^2. We can factor this quadratic using the AC method, where A*C = 5*(-32) = -160 and we need two numbers that multiply to -160 and add up to -12 (the coefficient of qr).Split and Rearrange Middle Term: The two numbers that multiply to -160 and add up to -12 are -20 and 8. So we can rewrite the middle term -12qr as -20qr + 8qr. The expression now becomes 5q^2 - 20qr + 8qr - 32r^2.Group and Factor Common Terms: We can now group the terms: (5q^2 - 20qr) + (8qr - 32r^2) and factor out the common factors from each group. From the first group, we can factor out 5q, and from the second group, we can factor out 8r.Identify Common Factor: After factoring out the common factors, we get 5q(q - 4r) + 8r(q - 4r). We can see that (q - 4r) is a common factor.Factor Out Common Factor: We factor out the common factor (q - 4r) to get (q - 4r)(5q + 8r).Substitute Back and Simplify: Finally, we substitute back p^(6) for q and h^(2) for r to get the completely factored form of the original expression: (p^(6) - 4h^(2))(5p^(6) + 8h^(2)).

Factor completely: $\newline$ $5 p^{12}-12 p^{6} h^{2}-32 h^{4}$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor completely:\newline5p12−12p6h2−32h4 5 p^{12}-12 p^{6} h^{2}-32 h^{4} 5p12−12p6h2−32h4\newlineAnswer:

Factor completely: $\newline$ $5 p^{12}-12 p^{6} h^{2}-32 h^{4}$ $\newline$ Answer: