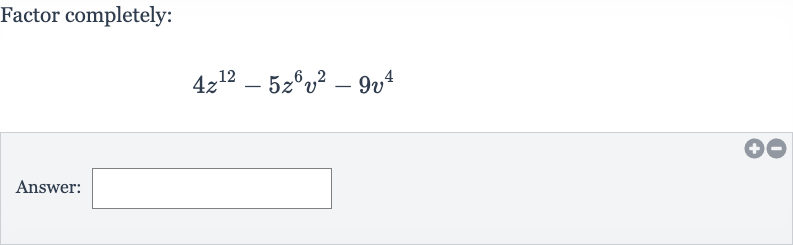
Factor completely: 4z^(12)-5z^(6)v^(2)-9v^(4) Answer:

Question

Factor completely:  4z^(12)-5z^(6)v^(2)-9v^(4) Answer:

Bytelearn · Accepted Answer

Identify common factor: Identify the common factor in the polynomial. The polynomial 4z^(12)-5z^(6)v^(2)-9v^(4) does not have a common factor across all terms, but we can observe that each term is a multiple of a power of z or v. We will look for a pattern or a common binomial factor that might help us factor by grouping or another method.Pattern or grouping: Look for a pattern or grouping method. We can try to factor by grouping, which involves rearranging the terms and factoring out the greatest common factor from each group. However, in this case, there is no clear grouping that will simplify the polynomial. Instead, we notice that the polynomial is a quadratic in form with respect to z^6. Let's rewrite the polynomial in terms of u = z^6.Substitute and rewrite: Substitute u for z^6 and rewrite the polynomial. Let u = z^6. Then the polynomial becomes 4u^2 - 5uv^2 - 9v^4. This is a quadratic in u, which we can attempt to factor.Factor quadratic in u: Factor the quadratic in u. We are looking for two numbers that multiply to (4)(-9v^4) = -36v^4 and add up to -5v^2. These numbers are -9v^2 and 4v^2. We can now rewrite the middle term -5uv^2 as -9uv^2 + 4uv^2 and factor by grouping.Factor by grouping: Factor by grouping. Rewrite the quadratic as 4u^2 - 9uv^2 + 4uv^2 - 9v^4. Now, group the terms: (4u^2 - 9uv^2) + (4uv^2 - 9v^4) Factor out the greatest common factor from each group: u(4u - 9v^2) + v^2(4u - 9v^2) Now we can factor out the common binomial factor (4u - 9v^2): (u + v^2)(4u - 9v^2)Substitute back in: Substitute z^6 back in for u. Replace u with z^6 in the factored form: (z^6 + v^2)(4z^6 - 9v^2) This is the completely factored form of the original polynomial.

Factor completely: $\newline$ $4 z^{12}-5 z^{6} v^{2}-9 v^{4}$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor completely:\newline4z12−5z6v2−9v4 4 z^{12}-5 z^{6} v^{2}-9 v^{4} 4z12−5z6v2−9v4\newlineAnswer:

Factor completely: $\newline$ $4 z^{12}-5 z^{6} v^{2}-9 v^{4}$ $\newline$ Answer: