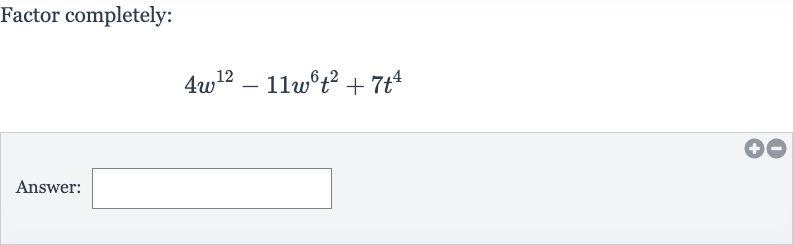Factor completely: 4w^(12)-11w^(6)t^(2)+7t^(4) Answer:

Question

Factor completely:  4w^(12)-11w^(6)t^(2)+7t^(4) Answer:

Bytelearn · Accepted Answer

Identify Structure of Polynomial: Identify the structure of the polynomial. The given polynomial is a trinomial in the form of aw^2 + bw + c, where the variable w is replaced by w^6 and the variable c is replaced by t^2.Look for Common Factor: Look for a common factor in all three terms. There is no common factor in all three terms, so we proceed to factor by grouping or other methods suitable for trinomials.Use Substitution to Simplify: Since the polynomial does not factor easily by grouping or simple trinomial factoring methods, we can try to use substitution to simplify the expression. Let's substitute u = w^6, then the polynomial becomes 4u^2 - 11ut + 7t^2.Factor Quadratic in Terms: Factor the quadratic in terms of u and t. We are looking for two numbers that multiply to (4)(7t^2) = 28t^2 and add up to -11t. These numbers are -4t and -7t.Write as Product of Binomials: Write the polynomial as a product of two binomials using the numbers found in Step 4. 4u^2 - 11ut + 7t^2 = (4u - 7t)(u - t)Substitute Back for Factorization: Substitute back w^6 for u to get the factorization in terms of w and t. (4u - 7t)(u - t) becomes (4w^6 - 7t)(w^6 - t).Check Factorization by Expanding: Check the factorization by expanding the factors to see if we get the original polynomial. (4w^6 - 7t)(w^6 - t) = 4w^12 - 4w^6t - 7tw^6 + 7t^2 = 4w^12 - 11w^6t + 7t^2

Factor completely: $\newline$ $4 w^{12}-11 w^{6} t^{2}+7 t^{4}$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor completely:\newline4w12−11w6t2+7t4 4 w^{12}-11 w^{6} t^{2}+7 t^{4} 4w12−11w6t2+7t4\newlineAnswer:

Factor completely: $\newline$ $4 w^{12}-11 w^{6} t^{2}+7 t^{4}$ $\newline$ Answer: