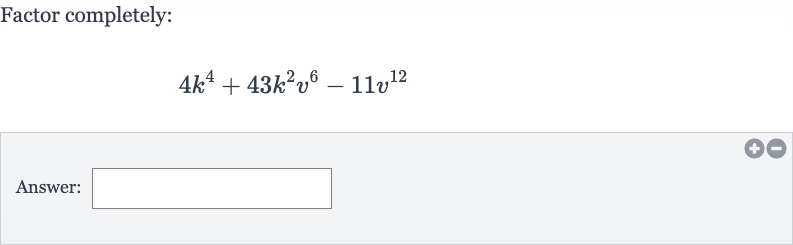
Factor completely: 4k^(4)+43k^(2)v^(6)-11v^(12) Answer:

Question

Factor completely:  4k^(4)+43k^(2)v^(6)-11v^(12) Answer:

Bytelearn · Accepted Answer

Identify Type and Factors: Identify the type of polynomial and look for common factors. The given polynomial is a quadratic in form with respect to k^2, where k^2 is the variable and v^6 is treated as a constant. There are no common factors for all terms.Set Up Quadratic Form: Set up the polynomial as a quadratic in terms of k^2. Let's rewrite the polynomial by substituting k^2 with a new variable, say m. So the polynomial becomes: 4m^2 + 43m - 11v^6, where m = k^2.Factor the Quadratic: Factor the quadratic polynomial. We need to find two numbers that multiply to (4)(-11v^6) = -44v^6 and add up to 43. These numbers are 44 and -1. Rewrite the middle term using these two numbers: 4m^2 + 44m - m - 11v^6 Group the terms to factor by grouping: (4m^2 + 44m) - (m + 11v^6) Factor out the common factors in each group: 4m(m + 11) - v^6(m + 11) Now factor out the common binomial factor (m + 11): (m + 11)(4m - v^6)Substitute Back: Substitute back k^2 for m. Replace m with k^2 in the factored form: (k^2 + 11)(4k^2 - v^6)Check Factored Form: Check the factored form by expanding it to ensure it matches the original polynomial. Expanding (k^2 + 11)(4k^2 - v^6) gives: 4k^4 - k^2v^6 + 44k^2 - 11v^6 Combine like terms: 4k^4 + (44k^2 - k^2v^6) - 11v^6 Since 44k^2 - k^2v^6 does not simplify to 43k^2v^6, we have made a mistake.

Factor completely: $\newline$ $4 k^{4}+43 k^{2} v^{6}-11 v^{12}$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor completely:\newline4k4+43k2v6−11v12 4 k^{4}+43 k^{2} v^{6}-11 v^{12} 4k4+43k2v6−11v12\newlineAnswer:

Factor completely: $\newline$ $4 k^{4}+43 k^{2} v^{6}-11 v^{12}$ $\newline$ Answer: