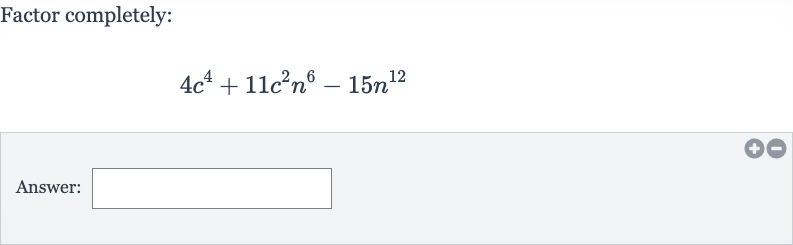
Factor completely: 4c^(4)+11c^(2)n^(6)-15n^(12) Answer:

Question

Factor completely:  4c^(4)+11c^(2)n^(6)-15n^(12) Answer:

Bytelearn · Accepted Answer

Identify Common Factors: Identify the polynomial and look for common factors. We have the polynomial 4c^(4) + 11c^(2)n^(6) - 15n^(12). We need to check if there is any common factor that can be factored out from all terms. In this case, there is no common factor across all terms.Recognize Quadratic Form: Recognize the polynomial as a quadratic in form. The polynomial can be seen as a quadratic in terms of c^(2), where c^(2) is the variable and n^(6) is a constant. The polynomial then takes the form of Ac^(4) + Bc^(2) + C, where A = 4, B = 11n^(6), and C = -15n^(12).Apply Quadratic Formula: Apply the quadratic formula to factor the polynomial. The quadratic formula for factoring Ax^2 + Bx + C is based on finding two numbers that multiply to A*C and add up to B. In this case, we need to find two numbers that multiply to (4)(-15n^(12)) = -60n^(12) and add up to 11n^(6).Find Suitable Numbers: Find two numbers that satisfy the conditions. We are looking for two numbers that multiply to -60n^(12) and add up to 11n^(6). These numbers are 20n^(6) and -3n^(6). We can check this by multiplying and adding them: (20n^(6))(-3n^(6)) = -60n^(12) and 20n^(6) - 3n^(6) = 17n^(6), which does not add up to 11n^(6). There is a mistake here.

Factor completely: $\newline$ $4 c^{4}+11 c^{2} n^{6}-15 n^{12}$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor completely:\newline4c4+11c2n6−15n12 4 c^{4}+11 c^{2} n^{6}-15 n^{12} 4c4+11c2n6−15n12\newlineAnswer:

Factor completely: $\newline$ $4 c^{4}+11 c^{2} n^{6}-15 n^{12}$ $\newline$ Answer: