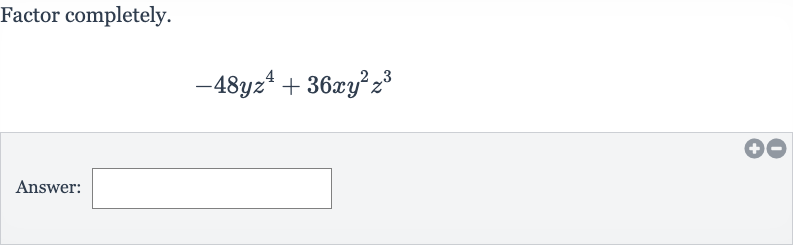AI tutor
Full solution
Q. Factor completely.Answer:
- Identify GCF: Identify the greatest common factor (GCF) of the terms in the expression and .The GCF is the product of the smallest powers of common factors in the terms. Both terms have a factor of , , and .GCF =
- Factor out GCF: Factor out the GCF from each term in the expression.
- Combine factored terms: Combine the factored terms into a single expression.
- Check for factors: Check for any additional common factors or factorable expressions within the parentheses.The terms inside the parentheses, and , do not have any common factors, and the expression inside the parentheses is not factorable.