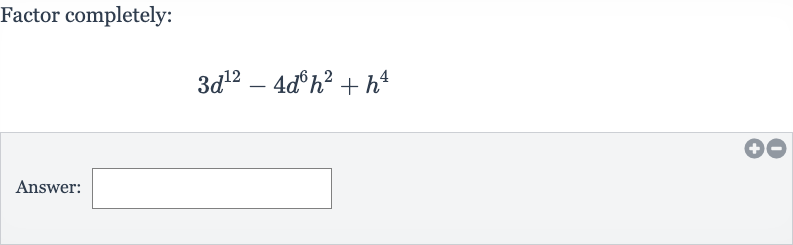Factor completely: 3d^(12)-4d^(6)h^(2)+h^(4) Answer:

Question

Factor completely:  3d^(12)-4d^(6)h^(2)+h^(4) Answer:

Bytelearn · Accepted Answer

Identify Common Factor: Identify the common factor in each term. The expression is a trinomial in the form of a cubic polynomial with respect to d^6. We can try to factor by grouping or look for a pattern that resembles a known factored form. In this case, we notice that each term is a power of d^6 or h^2, suggesting that we might be able to factor this as a sum or difference of cubes.Rewrite as Cubes: Rewrite the expression as a difference of cubes if possible. We can rewrite the expression as (d^6)^2 - 2*(d^6)*(h^2) + (h^2)^2. This resembles the square of a binomial, (a - b)^2 = a^2 - 2ab + b^2. Here, a = d^6 and b = h^2.Factor as Binomial: Factor the expression as the square of a binomial. Using the pattern from Step 2, we can write the expression as (d^6 - h^2)^2. This is the square of the binomial (d^6 - h^2).Factor Binomial Further: Factor the binomial further if possible. The binomial d^6 - h^2 is a difference of squares, which can be factored as (d^3 + h)(d^3 - h).Combine Factors: Combine the factors to write the final factored form. The completely factored form of the expression is the square of the binomial we found in Step 4, which is ((d^3 + h)(d^3 - h))^2.

Factor completely: $\newline$ $3 d^{12}-4 d^{6} h^{2}+h^{4}$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor completely:\newline3d12−4d6h2+h4 3 d^{12}-4 d^{6} h^{2}+h^{4} 3d12−4d6h2+h4\newlineAnswer:

Factor completely: $\newline$ $3 d^{12}-4 d^{6} h^{2}+h^{4}$ $\newline$ Answer: