AI tutor
Full solution
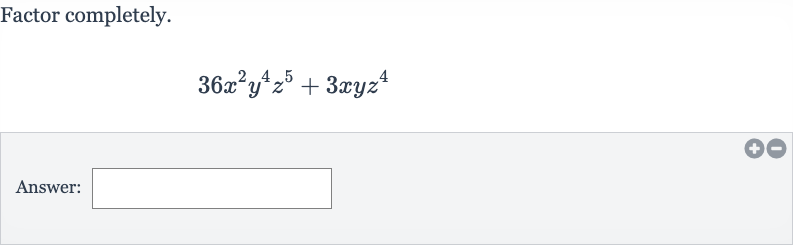
Q. Factor completely.Answer:
- Find GCF: To factor the expression completely, we first look for the greatest common factor (GCF) of the two terms and .
- Divide by GCF: The GCF of and is because is the largest integer that divides both and , is the highest power of that divides both and , is the highest power of that divides both and , and is the highest power of that divides both and .
- Write as Product: We divide each term by the GCF to find the other factor. and .
- Check Factored Expression: Now we can write the original expression as the product of the GCF and the other factor. .
- Check Factored Expression: Now we can write the original expression as the product of the GCF and the other factor. .We check to ensure that the factored expression, when expanded, gives us the original expression..