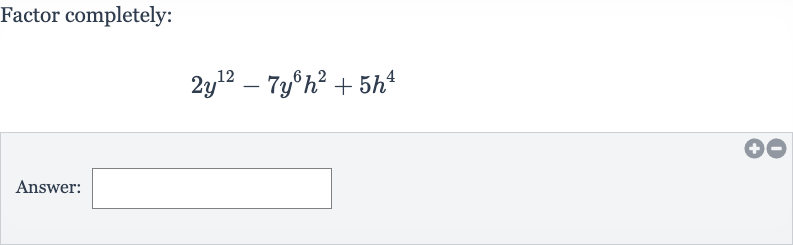Factor completely: 2y^(12)-7y^(6)h^(2)+5h^(4) Answer:

Question

Factor completely:  2y^(12)-7y^(6)h^(2)+5h^(4) Answer:

Bytelearn · Accepted Answer

Identify Factor: Identify the common factor in each term. In this case, there is no common factor across all three terms.Pattern or Grouping: Look for patterns or factor by grouping. Since there are three terms, we can consider if the polynomial is a quadratic in disguise with respect to y^6. Let's substitute y^6 with z and rewrite the polynomial. Let z = y^6. Then the polynomial becomes 2z^2 - 7zh + 5h^4.Factor Quadratic Polynomial: Factor the quadratic polynomial in z. We are looking for two numbers that multiply to 2*5h^4 (10h^4) and add up to -7h. These numbers are -2h and -5h. 2z^2 - 7zh + 5h^4 can be factored as (2z - 5h)(z - h).Substitute Back: Substitute y^6 back in for z. Replace z with y^6 in the factored form to get (2y^6 - 5h)(y^6 - h).Check Factored Form: Check the factored form by expanding it to ensure it matches the original polynomial. (2y^6 - 5h)(y^6 - h) = 2y^6 * y^6 + 2y^6 * (-h) - 5h * y^6 - 5h * (-h) = 2y^12 - 2y^6h - 5y^6h + 5h^4 = 2y^12 - 7y^6h + 5h^4 This matches the original polynomial, so the factoring is correct.

Factor completely: $\newline$ $2 y^{12}-7 y^{6} h^{2}+5 h^{4}$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor completely:\newline2y12−7y6h2+5h4 2 y^{12}-7 y^{6} h^{2}+5 h^{4} 2y12−7y6h2+5h4\newlineAnswer:

Factor completely: $\newline$ $2 y^{12}-7 y^{6} h^{2}+5 h^{4}$ $\newline$ Answer: