AI tutor
Full solution
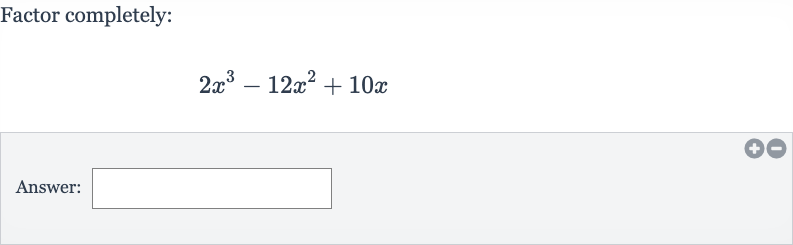
Q. Factor completely:Answer:
- Identify GCF: Identify the greatest common factor (GCF) of the terms in the polynomial . The GCF of , , and is , since is the largest expression that divides each term evenly.
- Factor GCF: Factor out the GCF from each term in the polynomial.
- Factor Quadratic: Factor the quadratic expression . We look for two numbers that multiply to and add up to . These numbers are and .
- Combine Factors: Combine the GCF with the factored form of the quadratic expression to get the final factored form of the original polynomial.