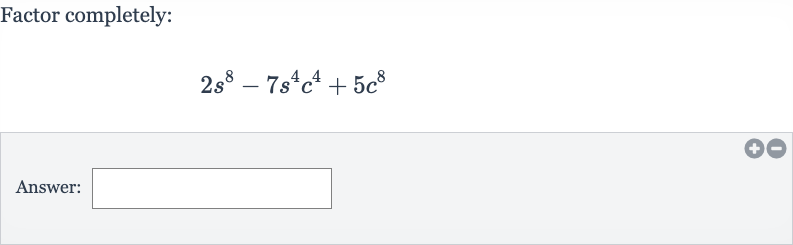Factor completely: 2s^(8)-7s^(4)c^(4)+5c^(8) Answer:

Question

Factor completely:  2s^(8)-7s^(4)c^(4)+5c^(8) Answer:

Bytelearn · Accepted Answer

Recognize Quadratic Form: Recognize the polynomial as a quadratic in form. The given polynomial 2s^(8)-7s^(4)c^(4)+5c^(8) can be seen as a quadratic in terms of s^(4) where s^(4) is the variable and c^(4) is a constant.Substitute New Variable: Substitute s^(4) with a new variable to simplify the expression. Let's substitute s^(4) with a new variable, say 'u'. So the expression becomes 2u^2 - 7uc^4 + 5c^8.Factor Quadratic Expression: Factor the quadratic expression. Now we factor the quadratic expression 2u^2 - 7uc^4 + 5c^8 as if it were a regular quadratic equation. We are looking for two numbers that multiply to 2*5c^8 (which is 10c^8) and add up to -7c^4.Find Factors: Find the factors of the quadratic expression. The two numbers that work are -2c^4 and -5c^4 because (-2c^4)*(-5c^4) = 10c^8 and (-2c^4) + (-5c^4) = -7c^4. So we can write the quadratic as 2u^2 - 2uc^4 - 5uc^4 + 5c^8.Factor by Grouping: Factor by grouping. Now we group the terms to factor by grouping: (2u^2 - 2uc^4) - (5uc^4 - 5c^8). We can factor out a common factor from each group: 2u(u - c^4) - 5c^4(u - c^4).Factor Common Factor: Factor out the common binomial factor. We notice that (u - c^4) is a common factor in both groups, so we factor it out: (u - c^4)(2u - 5c^4).Substitute Back: Substitute back s^(4) for u. Now we substitute back s^(4) for u to get the factorization in terms of the original variables: (s^(4) - c^4)(2s^(4) - 5c^4).Recognize Difference of Squares: Recognize the difference of squares in the first factor. The first factor (s^(4) - c^4) is a difference of squares, which can be factored further as (s^2 + c^2)(s^2 - c^2).Recognize Another Difference of Squares: Recognize another difference of squares in the second factor of step 8. The second factor of the first factor (s^2 - c^2) is also a difference of squares, which can be factored further as (s + c)(s - c).Combine Factors: Combine all factors to write the final factorization. The complete factorization of the original polynomial is (s^2 + c^2)(s + c)(s - c)(2s^4 - 5c^4).

Factor completely: $\newline$ $2 s^{8}-7 s^{4} c^{4}+5 c^{8}$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor completely:\newline2s8−7s4c4+5c8 2 s^{8}-7 s^{4} c^{4}+5 c^{8} 2s8−7s4c4+5c8\newlineAnswer:

Factor completely: $\newline$ $2 s^{8}-7 s^{4} c^{4}+5 c^{8}$ $\newline$ Answer: