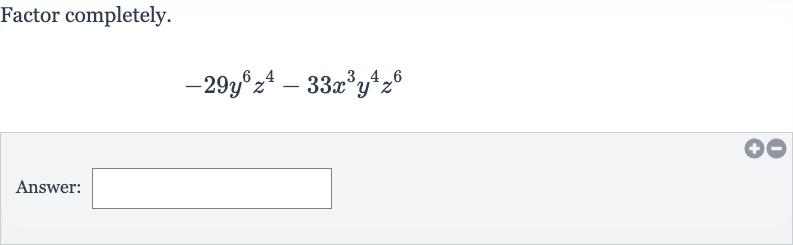Factor completely. -29y^(6)z^(4)-33x^(3)y^(4)z^(6) Answer:

Question

Factor completely.  -29y^(6)z^(4)-33x^(3)y^(4)z^(6) Answer:

Bytelearn · Accepted Answer

Identify GCF: Identify the greatest common factor (GCF) of the terms in the expression -29y^(6)z^(4)-33x^(3)y^(4)z^(6). The GCF is the product of the smallest powers of common factors in each term. Both terms have a common factor of y^(4) and z^(4), and the numerical GCF is 1 since 29 and 33 are both prime numbers and do not share any common factors.Factor Out GCF: Factor out the GCF from each term in the expression. The GCF we found is y^(4)z^(4), so we factor it out: -29y^(6)z^(4)-33x^(3)y^(4)z^(6) = y^(4)z^(4)(-29y^(2)-33x^(3)z^(2))Check Further Factoring: Check if the remaining expression inside the parentheses can be factored further. The terms inside the parentheses, -29y^(2) and -33x^(3)z^(2), do not have any common factors other than 1, and neither term is a perfect square or fits any special factoring patterns. Therefore, the expression inside the parentheses cannot be factored further.Write Final Form: Write down the final completely factored form of the original expression. The completely factored form of the expression is y^(4)z^(4)(-29y^(2)-33x^(3)z^(2)).

Factor completely. $\newline$ $-29 y^{6} z^{4}-33 x^{3} y^{4} z^{6}$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor completely.\newline−29y6z4−33x3y4z6 -29 y^{6} z^{4}-33 x^{3} y^{4} z^{6} −29y6z4−33x3y4z6\newlineAnswer:

Factor completely. $\newline$ $-29 y^{6} z^{4}-33 x^{3} y^{4} z^{6}$ $\newline$ Answer: