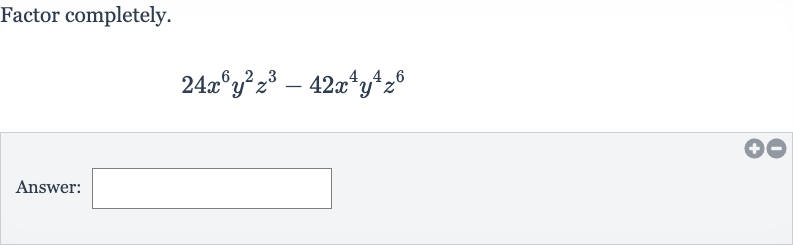AI tutor
Full solution
Q. Factor completely.Answer:
- Identify GCF: Identify the greatest common factor (GCF) of the two terms.Calculation: The GCF of and is . The GCF of and is . The GCF of and is . The GCF of and is .GCF =
- Factor Out GCF: Factor out the GCF from the original expression.Calculation:
- Check Factored Expression: Check the factored expression to ensure it is equivalent to the original expression when multiplied out.Calculation: This matches the original expression.