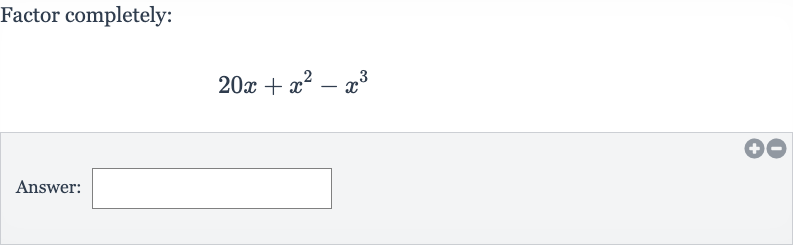AI tutor
Full solution
Q. Factor completely:Answer:
- Factor out 'x': First, we should look for any common factors in all terms of the polynomial .We can see that each term has an 'x' in it, so we can factor out an 'x' from the entire polynomial.Calculation:
- Rearrange terms in descending order: Now we have . We should rearrange the terms inside the parentheses in descending order of the powers of .Calculation:
- Factor quadratic expression: Next, we need to factor the quadratic expression . To do this, we look for two numbers that multiply to (the product of the coefficient of , which is , and the constant term, which is ) and add up to (the coefficient of ).The numbers that satisfy these conditions are and .Calculation:
- Combine factored terms: Finally, we combine the factored quadratic with the we factored out in the first step.Calculation: