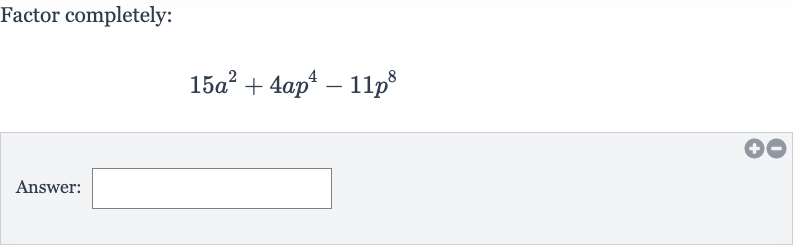Factor completely: 15a^(2)+4ap^(4)-11p^(8) Answer:

Question

Factor completely:  15a^(2)+4ap^(4)-11p^(8) Answer:

Bytelearn · Accepted Answer

Identify Common Factor: Identify the common factor in the given polynomial. The polynomial is 15a^(2)+4ap^(4)-11p^(8). We look for any common factors among the terms. There are no common factors other than 1.Use Factoring Technique: Look for patterns or use a factoring technique. Since there are no common factors, we need to look for patterns or use a factoring technique such as grouping, factoring by pairs, or using special products. However, this polynomial does not fit any of the common patterns (such as a difference of squares or a perfect square trinomial), and it does not appear to be factorable by grouping.Check for Special Patterns: Check if the polynomial is a difference of squares or cubes. The polynomial does not represent a difference of squares or cubes, as the terms do not fit the form a^2 - b^2 or a^3 - b^3.Factor by Substitution: Attempt to factor by substitution if applicable. This polynomial does not lend itself to easy substitution that would simplify the factoring process.Conclude Factorization: Conclude about the factorization of the polynomial. Since the polynomial does not have a common factor, does not fit any special patterns, and cannot be factored by grouping or substitution, we conclude that the polynomial is already in its simplest form and cannot be factored further over the integers.

Factor completely: $\newline$ $15 a^{2}+4 a p^{4}-11 p^{8}$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor completely:\newline15a2+4ap4−11p8 15 a^{2}+4 a p^{4}-11 p^{8} 15a2+4ap4−11p8\newlineAnswer:

Factor completely: $\newline$ $15 a^{2}+4 a p^{4}-11 p^{8}$ $\newline$ Answer: